Article contents
EXISTENCE OF MODELING LIMITS FOR SEQUENCES OF SPARSE STRUCTURES
Published online by Cambridge University Press: 07 March 2019
Abstract
A sequence of graphs is FO-convergent if the probability of satisfaction of every first-order formula converges. A graph modeling is a graph, whose domain is a standard probability space, with the property that every definable set is Borel. It was known that FO-convergent sequence of graphs do not always admit a modeling limit, but it was conjectured that FO-convergent sequences of sufficiently sparse graphs have a modeling limits. Precisely, two conjectures were proposed:
1. If a FO-convergent sequence of graphs is residual, that is if for every integer d the maximum relative size of a ball of radius d in the graphs of the sequence tends to zero, then the sequence has a modeling limit.
2. A monotone class of graphs
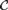 ${\cal C}$ has the property that every FO-convergent sequence of graphs from
${\cal C}$ has the property that every FO-convergent sequence of graphs from 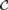 ${\cal C}$ has a modeling limit if and only if
${\cal C}$ has a modeling limit if and only if 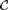 ${\cal C}$ is nowhere dense, that is if and only if for each integer p there is
${\cal C}$ is nowhere dense, that is if and only if for each integer p there is 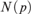 $N\left( p \right)$ such that no graph in
$N\left( p \right)$ such that no graph in 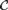 ${\cal C}$ contains the pth subdivision of a complete graph on
${\cal C}$ contains the pth subdivision of a complete graph on 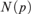 $N\left( p \right)$ vertices as a subgraph.
$N\left( p \right)$ vertices as a subgraph.
In this article we prove both conjectures. This solves some of the main problems in the area and among others provides an analytic characterization of the nowhere dense–somewhere dense dichotomy.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019
References
REFERENCES
- 5
- Cited by


