Article contents
Existence of classes and value specification of variables
Published online by Cambridge University Press: 12 March 2014
Extract
In mathematics, when we want to introduce classes which fulfill certain conditions, we usually prove beforehand that classes fulfilling such conditions do exist, and that such classes are uniquely determined by the conditions. The statements which state such unicity and existence of classes are in mathematical logic consequences of the principles of extensionality and class existence. In order to illustrate how these principles enable us to introduce classes into systems of mathematical logic, let us consider the manner in which Gödel introduces classes in his book on set theory.
For instance, before introducing the definition of the non-ordered pair of two classes
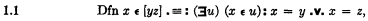
Gödel puts down as its justification the following two axioms:
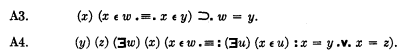
By A4, for every two classes y and z there exists at least one non-ordered pair w of them; and by A3, w is uniquely determined in A4.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1950
References
2 Godel, Kurt, The consistency of the continuum-hypothesis (1940, Princeton)Google Scholar. On p. 12 he says: “A special class is introduced by a defining postulate ϕ(A), where ϕ is a proposi-tional function containing only previously defined symbols and it has to be proved first that there is exactly one class A, such that ϕ (A).”
3 Ibid., p. 3. Gödel uses two kinds of variables, ‘X,’ ‘Y,’ ‘Z,’… as variables for all classes; ‘x,’ ‘y,’ ‘z’ … as variables which can be members of other classes. But it is easily seen that the second kind need not be taken as primitive. They can be defined in terms of the first kind by contextual definitions such as
etc. In order to facilitate comparison with other systems, I have retained only the first kind (general class variables), imagining that the second kind had been eliminated by such definitions. I have used small instead of capital latin letters as general class variables.
Strictly speaking, the way I state the definition 1.1 here is not correct, because it corresponds rather to Gödel's definition 3.1 on p. 11, ibid. However, as is remarked there under 3.1, this extension can easily be made.
4 Cf., e.g., the inference in the proofs of 7.15, 7.16, and 7.17 on pp. 24–25, ibid, that a statement is true of the class of all ordinal numbers if it is true for all values of a variable. See also the inference in the proofs of 2.31–2.8 on p. 9, ibid, that a statement is true for all n-tuplets (n ϕ 2) since it is true for all membership eligible classes.
5 At most places, the notation in this paper will follow Quine's, Mathematical logic (New York, 1940)Google Scholar, which will be referred to by the abbreviation ‘ML.’
More accurately, Dfn 1.1 should be supplemented with rules explaining, e.g., ‘[yz] ϵ x’ and ‘x = [yz]’ as well as ‘x ϵ [yz]’ before one can speak of substituting an abstract for a variable a in an arbitrary formula ϕ. We can use rules such as
6 Ibid., p. 3. He uses capital letters. But see footnote 3 of the present paper.
7 By ‘elementary logic’ I mean that portion of logic which comprises the prepositional calculus, the restricted functional calculus, and the principles of substitutivity and reflexivity for identity. In what follows, I shall make use of the metatheorems and theorems of elementary logic proved in ML. Starred and daggered numerals will be employed as in ML to refer to its metatheorems and theorems. For brevity, I have used in the next proof some notations which differ from that of ML. *220 used in the next proof should be proved with a proof somewhat different from its proof in ML. We can obtain such a proof by using the theory of identity and the definition of ‘w = [yz]’ as given under footnote 5.
8 In ML, ⊦ ⌜α ϵ V ≡ (∃γ) (α ϵ γ)⌝. See p. 178, †255.
9 It would seem relevant to point out the close connection between D9′ and another way of introducing class names into set theory by contextual definitions—namely by using a description operator. In a system which contains such an operator, abstracts can be introduced by the direct definition: ![]() for ⌜(וη)(α)(α ϵ η ≡ ϕ)⌝. Using A3 and EC and the standard theorems for the symbol ‘ו’ we easily obtain, by elementary logic, a metatheorem answering to D9′.
for ⌜(וη)(α)(α ϵ η ≡ ϕ)⌝. Using A3 and EC and the standard theorems for the symbol ‘ו’ we easily obtain, by elementary logic, a metatheorem answering to D9′.
10 See, e.g., Gödel, op. cit., Chapters 1–2.
11 In the following two proofs, we are assuming that abstracts have been introduced by D9″.
12 For the dispensability of *102 in ML, see this Journal, vol. 6, p. 23. After we have the five principles, metatheorems and theorems involving NN variables can be proved as those with general variables are proved in ML.
The referee has pointed out to me that the content of this paragraph is a direct consequence of Gödel's completeness theorem for the restricted functional calculus. Thus, let ϕ be any formula provable in the restricted functional calculus. Then by Gödel's theorem ϕ is valid when its variables are interpreted as ranging over an arbitrary domain D. Now let D′ be any subset of D, and let ϕ′ be the formula which is obtained from ϕ by restricting the range of the variables to be D′, according to the schema DV stated above. Since D was arbitrary the formula ϕ′ will be valid too; and hence, by Gödel's theorem, ϕ′ will be provable. But this is precisely the conclusion to be proved.
The present proof is still of some value, however, since it furnishes an effective method for transforming a formal proof of some ϕ into a formal proof of ϕ′.
13 Added October 24, 1949: I have found that the argument described in the preceding footnote is not correct. Thus let ϕ be ∼(α)(ψ▪∼ψ) and ϕ′ be ∼(α)(P(α) ⊃▪ ψ▪∼ψ). Then ϕ is valid but ϕ′ is not valid in domains where P(α) is always false. Moreover, the last two lines in the proof of *104′ are also in error, because we cannot prove the trivial case ![]() , where
, where ![]() is not free in ϕ. In order to prove it, we need an additional principle: AP. If a is not free in ϕ, then ⊢(α)(P(α) ⊃ ϕ) ⊃ ϕ.
is not free in ϕ. In order to prove it, we need an additional principle: AP. If a is not free in ϕ, then ⊢(α)(P(α) ⊃ ϕ) ⊃ ϕ.
Then we can replace the last two lines in the proof of *104′ by the following lines. If α′ is free in ϕ′, by DU and the definition of closure (using *119 and *123 if necessary),
If α′ is not free in ϕ′, apply AP first.
It should be noted that, by *161 and *100, AP is equivalent to the assertion that ⊢ (∃α)P(α). After we add AP, we can also fix up the argument described in the preceding footnote as follows. By the argument described there, if ϕ is provable in the restricted functional calculus, then (∃α)P(α) ⊃ ϕ′ is provable in it. As we have that ⊢ (∃α)P(α), ϕ′ is therefore also provable.
- 1
- Cited by


