Article contents
Embeddability and the word problem
Published online by Cambridge University Press: 12 March 2014
Extract
Let 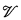 be a finitely presented variety with operations Ω and let
be a finitely presented variety with operations Ω and let 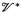 be the variety having the same set of operations Ω but defined by the empty set of identities. A partial
be the variety having the same set of operations Ω but defined by the empty set of identities. A partial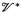 -algebra
-algebra 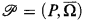 is a set P with a set of mappings
is a set P with a set of mappings 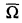 containing for each n-ary operation f of Ω a mapping
containing for each n-ary operation f of Ω a mapping 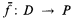 , where D ⊆ Pn. An incomplete
, where D ⊆ Pn. An incomplete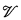 -algebra is a partial
-algebra is a partial 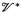 -algebra
-algebra 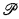 which satisfies the defining identities of
which satisfies the defining identities of 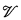 , insofar as they can be applied to the partial operations of
, insofar as they can be applied to the partial operations of 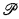 (Trevor Evans [4, p. 67]). We call an incomplete
(Trevor Evans [4, p. 67]). We call an incomplete 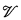 -algebra a partial Evans
-algebra a partial Evans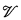 -algebra if it can be embedded in a member of the variety
-algebra if it can be embedded in a member of the variety 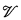 .
.
If the class of all partial Evans 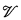 -algebras is (first-order) finitely axiomatizable, then the word problem for the variety
-algebras is (first-order) finitely axiomatizable, then the word problem for the variety 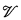 is solvable. (Evans [4, 5]). In 1953 Evans [5, p. 79] raised the question of whether the converse is true. In this paper we show that the answer is in the negative.
is solvable. (Evans [4, 5]). In 1953 Evans [5, p. 79] raised the question of whether the converse is true. In this paper we show that the answer is in the negative.
Let CSg denote the variety of commutative semigroups. We call an incomplete CSg-algebra an incomplete commutative semigroup and we call a partial Evans CSg-algebra a partial Evans commutative semigroup. It is known (A. I. Malcev [9] see also Evans [6]) that the variety of commutative semigroups has solvable word problem. We show (Theorem 1) that the class of all partial Evans commutative semigroups is not finitely axiomatizable. Therefore the solvability of the word problem for the variety of commutative semigroups does not imply finite axiomatizability of the class of all partial Evans commutative semigroups.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1995
References
REFERENCES
- 4
- Cited by


