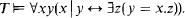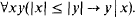Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Guier, Jorge I.
2001.
Boolean products of real closed valuation rings and fields.
Annals of Pure and Applied Logic,
Vol. 112,
Issue. 2-3,
p.
119.
Guzy, Nicolas
2005.
p-Convexly valued rings.
Journal of Pure and Applied Algebra,
Vol. 199,
Issue. 1-3,
p.
111.
Kulpeshov, Beibut Sh.
and
Macpherson, H. Dugald
2005.
Minimality conditions on circularly ordered structures.
MLQ,
Vol. 51,
Issue. 4,
p.
377.
Mellor, T.
2006.
Imaginaries in real closed valued fields.
Annals of Pure and Applied Logic,
Vol. 139,
Issue. 1-3,
p.
230.
Wencel, Roman
2013.
On the strong cell decomposition property for weakly o-minimal structures.
Mathematical Logic Quarterly,
Vol. 59,
Issue. 6,
p.
452.
Eivazloo, Jafar S.
and
Tari, Somayyeh
2014.
Tame properties of sets and functions definable in weakly o-minimal structures.
Archive for Mathematical Logic,
Vol. 53,
Issue. 3-4,
p.
433.
Lenzi, Giacomo
and
Marchioni, Enrico
2014.
An algebraic characterization of o-minimal and weakly o-minimal MV-chains.
Journal of Pure and Applied Algebra,
Vol. 218,
Issue. 1,
p.
90.
Aschenbrenner, Matthias
Dolich, Alf
Haskell, Deirdre
Macpherson, Dugald
and
Starchenko, Sergei
2015.
Vapnik-Chervonenkis density in some theories without the independence property, I.
Transactions of the American Mathematical Society,
Vol. 368,
Issue. 8,
p.
5889.
Eivazloo, Jafar S.
and
Tari, Somayyeh
2016.
Pseudo definably connected definable sets.
Mathematical Logic Quarterly,
Vol. 62,
Issue. 3,
p.
241.
Tari, Somayyeh
2017.
A note on prime models in weakly o‐minimal structures.
Mathematical Logic Quarterly,
Vol. 63,
Issue. 1-2,
p.
109.
Tari, Somayyeh
2017.
Some definable properties of sets in non-valuational weakly o-minimal structures.
Archive for Mathematical Logic,
Vol. 56,
Issue. 3-4,
p.
309.
Baĭzhanov, S. S.
and
Kulpeshov, B. Sh.
2018.
Preservation of ω-Categoricity In Expanding The Models of Weakly o-Minimal Theories.
Siberian Mathematical Journal,
Vol. 59,
Issue. 2,
p.
207.
Tari, Somayyeh
2021.
Strong cell decomposition property in o-minimal traces.
Archive for Mathematical Logic,
Vol. 60,
Issue. 1-2,
p.
135.
Krapp, Lothar Sebastian
Kuhlmann, Salma
and
Lehéricy, Gabriel
2021.
Strongly NIP almost real closed fields.
Mathematical Logic Quarterly,
Vol. 67,
Issue. 3,
p.
321.
Altayeva, A. B.
Kulpeshov, B. Sh.
and
Sudoplatov, S. V.
2021.
Algebras of Distributions of Binary Isolating Formulas for Almost ω-Categorical Weakly o-Minimal Theories.
Algebra and Logic,
Vol. 60,
Issue. 4,
p.
241.
IZBASAROV, A. A.
KULPESHOV, B. S.
and
EMELYANOV, D. Y.
2022.
ON (p, q)-SPLITTING FORMULAS IN ALMOST OMEGA-CATEGORICAL WEAKLY O-MINIMAL THEORIES.
Herald of the Kazakh-British technical university,
Vol. 19,
Issue. 2,
p.
20.
Ealy, Clifton F.
and
Maříková, Jana
2023.
Quantifier elimination for o-minimal structures expanded by a valuational cut.
Annals of Pure and Applied Logic,
Vol. 174,
Issue. 2,
p.
103206.
Tari, Somayyeh
2023.
A criterion for the strong cell decomposition property.
Archive for Mathematical Logic,
Vol. 62,
Issue. 7-8,
p.
871.
Kulpeshov, Beibut Shaiykovich
Pavlyuk, Inessa Ivanovna
and
Sudoplatov, Sergey Vladimirovich
2024.
Ранги и аппроксимации для семейств упорядоченных теорий.
Математические заметки,
Vol. 116,
Issue. 4,
p.
531.
Kulpeshov, B. Sh.
Pavlyuk, In. I.
and
Sudoplatov, S. V.
2024.
Ranks and Approximations for Families of Ordered Theories.
Mathematical Notes,
Vol. 116,
Issue. 3-4,
p.
669.