Published online by Cambridge University Press: 12 March 2014
Let 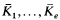 be p-adic closures of a countable Hilbertian field K. The main result of [EJ] asserts that the field
be p-adic closures of a countable Hilbertian field K. The main result of [EJ] asserts that the field 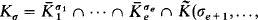
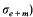 has the following properties for almost all σ1,…,σe + m ϵ G(K) (in the sense of the unique Haar measure on G(K)e+m):
has the following properties for almost all σ1,…,σe + m ϵ G(K) (in the sense of the unique Haar measure on G(K)e+m):
(a) Kσ is pseudo p-adically closed (abbreviation: PpC), i.e., each nonempty absolutely irreducible variety defined over Kσ has a Kσ-rational point, provided that it has a simple rational point in each p-adic closure of Kσ.
(b) G(Kσ) ≅ De,m, where De,m is the free profinite product 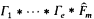 of e copies Γ1,…, Γe of G(ℚp) and a free profinite group
of e copies Γ1,…, Γe of G(ℚp) and a free profinite group 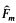 of rank m.
of rank m.
(c) Kσ has exactly e nonequivalent p-adic valuation rings. They are the restrictions Oσ1,…, Oσe of the unique p-adic valuation rings on 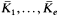 , respectively.
, respectively.
In this paper we show that this result is in a certain sense the best possible. More precisely, we first show that the class of fields which satisfy (a)–(c) above is elementary in the appropriate language 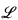 e(K), which is the ordinary first-order language of rings augmented by constant symbols for the elements of K and by e new unary relation symbols
e(K), which is the ordinary first-order language of rings augmented by constant symbols for the elements of K and by e new unary relation symbols 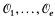 (interpreted as e p-adic valuation rings).
(interpreted as e p-adic valuation rings).