No CrossRef data available.
Article contents
Elementary embedding between countable Boolean algebras
Published online by Cambridge University Press: 12 March 2014
Abstract
For a complete theory of Boolean algebras T, let MT denote the class of countable models of T. For B1, B2 ∈ MT, let B1 ≤ B2 mean that B2 is elementarily embeddable in B2. Theorem 1. For every complete theory of Boolean algebras T, if T ≠ Tω, then ‹MT, ≤› is well-quasi-ordered. ∎ We define Tω. For a Boolean algebra B, let I(B) be the ideal of all elements of the form a + s such that B ↾ a is an atomic Boolean algebra and B ↾ s is an atomless Boolean algebra. The Tarski derivative of B is defined as follows: B(0) = B and B(n + 1) = B(n)/I(B(n)). Define Tω to be the theory of all Boolean algebras such that for every n ∈ ω, B(n) ≠ {0}. By Tarski [1949], Tω is complete. Recall that ‹A, < › is partial well-quasi-ordering, it is a partial quasi-ordering and for every {ai, ⃒ i ∈ ω} ⊆ A, there are i < j < ω such that ai ≤ aj. Theorem 2. 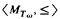 contains a subset M such that the partial orderings ‹M, ≤ ↾ M› and
contains a subset M such that the partial orderings ‹M, ≤ ↾ M› and 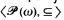 are isomorphic. ∎ Let M′0 denote the class of all countable Boolean algebras. For B1, B2 ∈ M′0, let B1 ≤′ B2 mean that B1 is embeddable in B2. Remark. ‹M′0, ≤′› is well-quasi-ordered. ∎ This follows from Laver's theorem [1971] that the class of countable linear orderings with the embeddability relation is well-quasi-ordered and the fact that every countable Boolean algebra is isomorphic to a Boolean algebra of a linear ordering.
are isomorphic. ∎ Let M′0 denote the class of all countable Boolean algebras. For B1, B2 ∈ M′0, let B1 ≤′ B2 mean that B1 is embeddable in B2. Remark. ‹M′0, ≤′› is well-quasi-ordered. ∎ This follows from Laver's theorem [1971] that the class of countable linear orderings with the embeddability relation is well-quasi-ordered and the fact that every countable Boolean algebra is isomorphic to a Boolean algebra of a linear ordering.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1991


