Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T09:10:42.476Z Has data issue: false hasContentIssue false
  • English
  • Français

DOMINIONS AND PRIMITIVE POSITIVE FUNCTIONS

Published online by Cambridge University Press:  05 February 2018

MIGUEL CAMPERCHOLI
MIGUEL CAMPERCHOLI*
Affiliation:
CIEM — FACULTAD DE MATEMÁTICA, ASTRONOMÍA Y FÍSICA (FA.M.A.F.) UNIVERSIDAD NACIONAL DE CÓRDOBA — CIUDAD UNIVERSITARIA CÓRDOBA 5000, ARGENTINAE-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let A ≤ B be structures, and 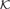${\cal K}$ a class of structures. An element b ∈ B is dominated by A relative to 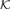${\cal K}$ if for all 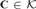${\bf{C}} \in {\cal K}$ and all homomorphisms g, g' : B → C such that g and g' agree on A, we have gb = g'b. Our main theorem states that if 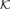${\cal K}$ is closed under ultraproducts, then A dominates b relative to 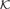${\cal K}$ if and only if there is a partial function F definable by a primitive positive formula in 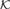${\cal K}$ such that FB(a1,…,an) = b for some a1,…,an ∈ A. Applying this result we show that a quasivariety of algebras 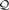${\cal Q}$ with an n-ary near-unanimity term has surjective epimorphisms if and only if 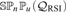$\mathbb{S}\mathbb{P}_n \mathbb{P}_u \left( {\mathcal{Q}_{{\text{RSI}}} } \right)$ has surjective epimorphisms. It follows that if 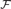${\cal F}$ is a finite set of finite algebras with a common near-unanimity term, then it is decidable whether the (quasi)variety generated by 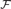${\cal F}$ has surjective epimorphisms.

Keywords

18A2003C0503C6003C4008C15epimorphismdominionepic substructureBeth definabilitydefinable functionIsbell’s Zigzag Theorem
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 1 , March 2018 , pp. 40 - 54
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bezhanishvili, G., Moraschini, T., and Raftery, J., Epimorphisms in varieties of residuated structures, submitted, 2016.Google Scholar
Blok, W. and Hoogland, E., The Beth property in algebraic logic. Studia Logica, vol. 83 (2006), pp. 49–90.CrossRefGoogle Scholar
Budkin, A., Dominions in quasivarieties of universal algebras. Studia Logica, vol. 78 (2004), no. 1–2, pp. 107–127.CrossRefGoogle Scholar
Budkin, A., Dominions of universal algebras and projective properties. Algebra and Logic, vol. 47 (2008), no. 5, pp. 304–313.Google Scholar
Burris, S. and Sankappanavar, H., A Course in Universal Algebra, Graduate Texts in Mathematics, Springer-Verlag, New York, 1981.CrossRefGoogle Scholar
Campercholi, M. and Vaggione, D., Semantical conditions for the definability of functions and relations. Algebra Universalis, vol. 76 (2016), no. 1, pp. 71–98.Google Scholar
Czelakowski, J. and Dziobiak, W., Congruence distributive quasivarieties whose finitely subdirectly irreducible members form a universal class. Algebra Universalis, vol. 27 (1990), no. 1, pp. 128–149.Google Scholar
Higgins, P., Epimorphisms and amalgams. Colloquium Mathematicae, vol. 56 (1988), no. 1, pp. 1–17.Google Scholar
Higgins, P., A short proof of Isbell’s zigzag theorem. Pacific Journal of Mathematics, vol. 144 (1990), no. 1, pp. 47–50.Google Scholar
Hodges, W., Model Theory, Encyclopedia of Mathematics and its Applications, Cambridge University Press, Cambridge, 1993.Google Scholar
Hoffman, P., A proof of Isbell’s zigzag theorem. Journal of the Australian Mathematical Society, vol. 84 (2008), pp. 229–232.Google Scholar
Howie, J., Fundamentals of Semigroup Theory, LMS Monographs, Clarendon Press, New York, 1995.CrossRefGoogle Scholar
Isbell, J., Epimorphisms and dominions, Proceedings of the Conference on Categorical Algebra: La Jolla 1965 (Eilenberg, S., Harrison, D. K., Röhrl, H., and MacLane, S., editors), Springer, Berlin, Heidelberg, 1966, pp. 232–246.CrossRefGoogle Scholar
Jónsson, B., Algebras whose congruence lattices are distributive. Mathematica Scandinavica, vol. 21 (1968), no. 1, pp. 110–121.Google Scholar
Philip, J., A proof of Isbell’s zig-zag theorem. Journal of Algebra, vol. 32 (1974), no. 2, pp. 328–331.CrossRefGoogle Scholar
Renshaw, J., On free products of semigroups and a new proof of Isbell’s zigzag theorem. Journal of Algebra, vol. 251 (2002), no. 1, pp. 12–15.CrossRefGoogle Scholar
Storrer, H., An algebraic proof of Isbell’s zigzag theorem. Semigroup Forum, vol. 12 (1976), pp. 83–88.Google Scholar
Vaggione, D., Infinitary Baker-Pixley Theorem, submitted, 2016.Google Scholar
Wasserman, D., Epimorphisms and dominions in varieties of lattices, Ph.D. thesis, University of California at Berkeley, 2001.Google Scholar