Hostname: page-component-5cf477f64f-xc2pj Total loading time: 0 Render date: 2025-04-08T01:02:36.915Z Has data issue: false hasContentIssue false
  • English
  • Français

DISJOINT AMALGAMATION IN LOCALLY FINITE AEC

Published online by Cambridge University Press:  21 March 2017

JOHN T. BALDWIN ,
MARTIN KOERWIEN  and
MICHAEL C. LASKOWSKI
JOHN T. BALDWIN
Affiliation:
DEPARTMENT OF MATHEMATICS, STATISTICS AND COMPUTER SCIENCE M/C 249 UNIVERSITY OF ILLINOIS AT CHICAGO 851 S. MORGAN STREET CHICAGO, IL60607, USAE-mail: [email protected]
MARTIN KOERWIEN
Affiliation:
UNIVERSITÄT WIENKURT GÖDEL RESEARCH CENTER FOR MATHEMATICAL LOGIC WÄHRINGER STRASSE 25, 1090WIEN, AUSTRIAE-mail: [email protected]
MICHAEL C. LASKOWSKI
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF MARYLAND COLLEGE PARK, MD20742, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce the concept of a locally finite abstract elementary class and develop the theory of disjoint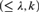$\left( { \le \lambda ,k} \right)$-amalgamation) for such classes. From this we find a family of complete 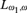${L_{{\omega _1},\omega }}$ sentences 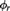${\phi _r}$ that a) homogeneously characterizes 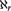${\aleph _r}$ (improving results of Hjorth [11] and Laskowski–Shelah [13] and answering a question of [21]), while b) the 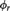${\phi _r}$ provide the first examples of a class of models of a complete sentence in ${L_{{\omega _1},\omega }}$ where the spectrum of cardinals in which amalgamation holds is other that none or all.

Keywords

03C4803C75characterize cardinalsamalgamationabstract elementary classesLω1ω
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 1 , March 2017 , pp. 98 - 119
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baldwin, J. T., Categoricity, University Lecture Notes, vol. 51, American Mathematical Society, Providence, RI, 2009.Google Scholar
Baldwin, J. T. and Boney, W., The Hanf number for amalgamation and joint embedding in AEC’s , Beyond First Order Model Theory, 2015, submitted.Google Scholar
Baldwin, J. T., Friedman, S., Koerwien, M., and Laskowski, C., Three red herrings around Vaught’s conjecture . Transactions of the American Mathematical Society, vol. 368 (2016), pp. 3673–3694.Google Scholar
Baldwin, J. T., Koerwien, M., and Souldatos, I., The joint embedding property and maximal models , Archive for Mathematical Logic, vol. 55 (2016), no. 3, 545–565.CrossRefGoogle Scholar
Baldwin, J. T. and Kolesnikov, A., Categoricity, amalgamation, and tameness . Israel Journal of Mathematics, vol. 170 (2009), pp. 411–443.CrossRefGoogle Scholar
Baldwin, J. T., Kolesnikov, A., and Shelah, S., The amalgamation spectrum, this JOURNAL, vol. 74 (2009), pp. 914–928.Google Scholar
Baldwin, J. T., Laskowski, M. C., and Shelah, S., Constructing many uncountable atomic models in ${\aleph _1}$ , this JOURNAL, vol. 81 (2016), pp. 1142–1162.Google Scholar
Baldwin, J. T. and Souldatos, I., Complete ${L_{{\omega _1},\omega }}$ -sentences with maximal models in multiple cardinalities, 2015, submitted.Google Scholar
Button, T. and Walsh, S., Ideas and results in model theory: Reference, realism, structure and categoricity, 2015, manuscript, http://faculty.sites.uci.edu/seanwalsh/files/2015/01/button-walsh-arXiv-submit.1150992.pdf.Google Scholar
Hart, B. and Shelah, S., Categoricity over P for first order T or categoricity for $\phi \in {{\rm{l}}_{{\omega _1}\omega }}$ can stop at ${\aleph _k}$ while holding for ${\aleph _0}, \ldots ,{\aleph _{k - 1}}$ . Israel Journal of Mathematics, vol. 70 (1990), pp. 219–235.Google Scholar
Hjorth, G., Knight’s model, its automorphism group, and characterizing the uncountable cardinals . Journal of Mathematical Logic, vol. 2 (2002), pp. 113–144.Google Scholar
Kolesnikov, A. and Lambie-Hanson, C., Hanf numbers for amalgamation of coloring classes, 2014, preprint.Google Scholar
Laskowski, M. C. and Shelah, S., On the existence of atomic models, this JOURNAL, vol. 58 (1993), pp. 1189–1194.Google Scholar
Malitz, J., The Hanf number for complete ${L_{{\omega _1},\omega }}$ sentences, The Syntax and Semantics of Infinitary Languages (Barwise, J., editor), LNM 72, Springer-Verlag, Heidelberg, 1968, pp. 166–181.Google Scholar
Shelah, S., Classification theory for nonelementary classes. I. the number of uncountable models of $\psi \in {L_{{\omega _1}\omega }}$ part A. Israel Journal of Mathematics, vol. 46 (1983), no. 3, pp. 212–240.Google Scholar
Shelah, S., Classification theory for nonelementary classes. II. the number of uncountable models of $\psi \in {L_{{\omega _1}\omega }}$ part B. Israel Journal of Mathematics, vol. 46 (1983), no. 3, pp. 241–271.Google Scholar
Shelah, S., Classification Theory for Abstract Elementary Classes, Studies in Logic, College Publications, London, 2009.Google Scholar
Shelah, S., Classification Theory for Abstract Elementary Classes: II. Studies in Logic, College Publications, London, 2010.Google Scholar
Shelah, S., Classification of nonelementary classes II, abstract elementary classes , Classification Theory (Chicago, IL, 1985), Proceedings of the USA–Israel Conference on Classification Theory (Baldwin, J. T., editor), Lecture Notes in Mathematics, vol. 1292, Springer, Berlin, 1987, pp. 419–497.Google Scholar
Souldatos, I., Characterizing the powerset by a complete (Scott) sentence . Fundamenta Mathematica, vol. 222 (2013), pp. 131–154.Google Scholar
Souldatos, I., Notes on cardinals that are characterizable by a complete (Scott) sentence . Notre Dame Journal of Formal Logic, vol. 55 (2013), pp. 533–551.Google Scholar