Published online by Cambridge University Press: 12 March 2014
Let 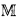 be an o-minimal expansion of the ordered field of real numbers
be an o-minimal expansion of the ordered field of real numbers 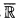 , and let S be an
, and let S be an 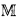 -definable subset (parameters allowed unless otherwise stated) of ℝn. In this note I investigate questions concerning the distribution of points on S with integer coordinates. My main theorem gives an estimate which, though probably far from best possible, at least shows that the o-minimal assumption does have diophantine consequences. This is, perhaps, surprising in view of the flexibility that we now seem to have in constructing o-minimal expansions of
-definable subset (parameters allowed unless otherwise stated) of ℝn. In this note I investigate questions concerning the distribution of points on S with integer coordinates. My main theorem gives an estimate which, though probably far from best possible, at least shows that the o-minimal assumption does have diophantine consequences. This is, perhaps, surprising in view of the flexibility that we now seem to have in constructing o-minimal expansions of 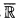 (see, e. g. [7], [8], [9]).
(see, e. g. [7], [8], [9]).