Published online by Cambridge University Press: 12 March 2014
For any A ⊂ R, the Banach game B(A) is the following infinite game on reals: Players I and II alternately play positive real numbers a1; a2, a3, a4,… such that for n > 1, an < an−1. Player I wins iff 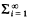 ai exists and is in A.
ai exists and is in A.
This type of game was introduced by Banach in 1935 in the Scottish Book [15], Problem 43. The (rather vague) problem which Banach posed was to characterize those sets A for which I (II) has a winning strategy in B(A). (There are three parts to Problem 43. In the first, Mazur defined a game G**(A) for every set A ⊂ R and conjectured that II has a winning strategy in G**(A) iff A is meager and I has a winning strategy in G**(A) iff A is comeager in some neighborhood; this conjecture was proved by Banach. Presumably Banach had this result in mind when he asked the question about B(A), and hoped for a similar type of characterization.) Incidentally, Problem 43 of the Scottish Book appears to be the first time infinite games of any sort were studied by mathematicians.
This paper will not provide the reader with any answer to Banach's question. I know of no nontrivial way to characterize when player I (or II) wins, and I suspect there is none. This paper is concerned with a different (also rather vague) question: For which sets A is the Banach game B(A) determined? To say that B(A) is determined means, of course, that one of the players has a winning strategy for B(A).