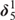Hostname: page-component-5cf477f64f-r2nwp Total loading time: 0 Render date: 2025-04-07T21:39:02.079Z Has data issue: false hasContentIssue false
  • English
  • Français

DESCRIPTIONS AND CARDINALS BELOW $\delta _5^1$

Published online by Cambridge University Press:  01 December 2016

STEVE JACKSON  and
FARID T. KHAFIZOV
STEVE JACKSON
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NORTH TEXAS DENTON, TX 76203-1430, USAE-mail: [email protected]
FARID T. KHAFIZOV
Affiliation:
DEPARTMENT OF MATHEMATICAL SCIENCES UNIVERSITY OF TEXAS AT DALLAS 800 WEST CAMPBELL ROAD RICHARDSON, TX 75080-3021, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Assuming AD, we show that all of the ordinals below 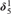$\delta _5^1$ represented by descriptions (c.f. [2], but also defined below) are cardinals. Using this analysis we also get a simple representation for the cardinal structure below 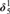$\delta _5^1$. As an application, we compute the cofinalitites of all cardinals below 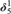$\delta _5^1$.

Keywords

03E60cardinalsdescriptionsdeterminacyprojective ordinals
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 4 , December 2016 , pp. 1177 - 1224
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Jackson, S., AD and the projective ordinals , Cabal Seminar 81–85, vol. 1333, Lecture Notes in Mathematics, Springer, Berlin, 1988, pp. 117–220.CrossRefGoogle Scholar
Jackson, S., A computation of ${\bf{\delta }}_5^1$ . Memoirs of the American Mathematical Society, vol. 140 (1999), no. 670, pp. 1–94.Google Scholar
Jackson, S., Structural consequences of AD , Handbook of Set Theory, vol. 3, Springer, Dordrecht, 2010, pp. 1753–1876.CrossRefGoogle Scholar
Kechris, A. S., AD and the projective ordinals , Cabal Seminar 76–77, vol. 689, Lecture Notes in Mathematics, Springer, Berlin, 1978, pp. 91–132.CrossRefGoogle Scholar
Moschovakis, Y. N., Descriptive Set Theory, vol. 100, Studies in logic, North–Holland, Amsterdam, 1980.Google Scholar
Solovay, R. M., A $\delta _3^1$ coding of the subsets of ωω . Cabal Seminar 76–77, vol. 689, Lecture Notes in Mathematics, Springer, Berlin, 1978, pp. 133–150.CrossRefGoogle Scholar