Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-19T09:51:03.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Degree spectra of prime models

Published online by Cambridge University Press:  12 March 2014

Barbara F. Csima
Barbara F. Csima*
Affiliation:
Department of Mathematics, Cornell University, New York 14853-4201, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract.

We consider the Turing degrees of prime models of complete decidable theories. In particular we show that every complete decidable atomic theory has a prime model whose elementary diagram is low. We combine the construction used in the proof with other constructions to show that complete decidable atomic theories have low prime models with added properties.

If we have a complete decidable atomic theory with all types of the theory computable, we show that for every degree d with 0 < d < 0', there is a prime model with elementary diagram of degree d. Indeed, this is a corollary of the fact that if T is a complete decidable theory and L is a computable set of c.e. partial types of T, then for any 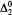degree d > 0, T has a d-decidable model omitting the nonprincipal types listed by L.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 2 , June 2004 , pp. 430 - 442
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chang, C. C. and Keisler, H. J., Model theory, 3rd ed., Studies in Logic and the Foundations of Mathematics, vol. 73, North-Holland, Amsterdam, 1990.Google Scholar
[2]Clote, P., A note on decidable model theory, Model theory and arithmetic, Lecture Notes in Mathematics, vol. 890, Springer, Berlin, 1981, pp. 134–142.CrossRefGoogle Scholar
[3]Csima, B. F., Hirschfeldt, D. R., Knight, J. F., and Soare, R. I., Bounding prime models, to appear.CrossRefGoogle Scholar
[4]Denisov, A. S., Homogeneous 0′-elements in structural pre-orders, Algebra and Logic, vol. 28 (1989), pp. 405–418.CrossRefGoogle Scholar
[5]Drobotun, B. N., Numerations of simple models, Siberian Mathematical Journal, vol. 18 (1977), no. 5, pp. 707–716 (1978).CrossRefGoogle Scholar
[6]Harizanov, V. S., Pure computable model theory, Handbook of recursive mathematics (Ershov, Yu. L., Goncharov, S. S., Nerode, A., and Remmel, J. B., editors), Studies in Logic and the Foundations of Mathematics, vol. 138-139, Elsevier Science, Amsterdam, 1998, pp. 3–114.Google Scholar
[7]Jockusch, C. G. Jr. and Soare, R. I., classes and degrees of theories, Transactions of the American Mathematical Society, vol. 173 (1972), pp. 33–56.Google Scholar
[8]Knight, J. F., Degrees coded in jumps of orderings, this Journal, vol. 51 (1986), pp. 1034–1042.Google Scholar
[9]Marker, D., Model theory, Springer-Verlag, New York, 2002.Google Scholar
[10]Millar, T. S., Foundations of recursive model theory, Annals of Mathematical Logic, vol. 13 (1978), pp. 45–72.CrossRefGoogle Scholar
[11]Millar, T. S., Omitting types, type spectrums, and decidability, this Journal, vol. 48 (1983), pp. 171–181.Google Scholar
[12]Miller, R. G., The -spectrum of a linear order, this Journal, vol. 66 (2001), pp. 470–486.Google Scholar
[13]Slaman, T., Relative to any nonrecursive set, Proceedings of the American Mathematical Society, vol. 126 (1998), pp. 2117–2122.CrossRefGoogle Scholar
[14]Soare, R. I., Recursively enumerable sets and degrees: A Study of Computable Functions and Computably Generated Sets, Springer-Verlag, Heidelberg, 1987.CrossRefGoogle Scholar
[15]Wehner, S., Enumerations, countable structures and Turing degrees, Proceedings of the American Mathematical Society, vol. 126 (1998), pp. 2131–2139.CrossRefGoogle Scholar