No CrossRef data available.
Article contents
Degree invariance in the Π10classes
Published online by Cambridge University Press: 12 March 2014
Abstract
Let  denote the collection of all Π10 classes, ordered by inclusion. A collection of Turing degrees in
denote the collection of all Π10 classes, ordered by inclusion. A collection of Turing degrees in  is called invariant over
is called invariant over  if there is some collection
if there is some collection 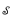 of Π10 classes representing exactly the degrees
of Π10 classes representing exactly the degrees  such that
such that 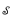 is invariant under automorphisms of
is invariant under automorphisms of  . Herein we expand the known degree invariant classes of
. Herein we expand the known degree invariant classes of  , previously including only {0} and the array noncomputable degrees, to include all highn and non-lown degrees for n > 2. This is a corollary to a very general definability result. The result is carried out in a substructure G of
, previously including only {0} and the array noncomputable degrees, to include all highn and non-lown degrees for n > 2. This is a corollary to a very general definability result. The result is carried out in a substructure G of  , within which the techniques used model those used by Cholak and Harrington [6] to obtain the same definability for the c.e. sets. We work back and forth between G and
, within which the techniques used model those used by Cholak and Harrington [6] to obtain the same definability for the c.e. sets. We work back and forth between G and  to show that this definability in G gives the desired degree invariance over
to show that this definability in G gives the desired degree invariance over  .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2011


