Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Selivanov, V. L.
1988.
Algorithmic complexity of algebraic systems.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 44,
Issue. 6,
p.
944.
Arslanov, M. M.
1989.
Completeness in the arithmetical hierarchy and fixed points.
Algebra and Logic,
Vol. 28,
Issue. 1,
p.
1.


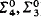 ), i.e. isomorphic to the lattice of
), i.e. isomorphic to the lattice of 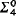 sets together with a unary predicate selecting out exactly the
sets together with a unary predicate selecting out exactly the 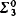 sets.
sets.