Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T06:30:18.550Z Has data issue: false hasContentIssue false
  • English
  • Français

The deduction theorem in a functional calculus of first order based on strict implication

Published online by Cambridge University Press:  12 March 2014

Ruth C. Barcan
Ruth C. Barcan*
Affiliation:
Yale University
Get access Rights & Permissions [Opens in a new window]

Extract

In a previous paper, a functional calculus based on strict implication was developed. That system will be referred to as S2. The system resulting from the addition of Becker's axiom 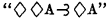will be referred to as S4. In the present paper we will shw that a restricted deduction theorem is provable in S4 or more precisely in a system equivalent to S4. We will also show that such a deduction theorem is not provable in S2.

The following theorems not derived in Symbolic logic will be required for the fundamental theorems XXVIII* and XXIX* of this paper. We will state most of them without proofs.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 11 , Issue 4 , December 1946 , pp. 115 - 118
Copyright
Copyright © Association for Symbolic Logic 1947

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 A functional calculus of first order based on strict implication, this Journal, vol. 11 (1946), pp. 1-16.

2 See Lewis, and Langford, , Symbolic logic, pp. 497–502.Google Scholar

3 Part of this paper was included in a dissertation written in partial fulfillment of the requirements for the Ph.D. degree in Philosophy at Yale University. I am grateful to Professor Frederic B. Fitch for his criticisms and suggestions.

4 Parry, W. T., The postulates for “strict implication,” Mind, vol. 43 (1934), pp. 78–80.CrossRefGoogle Scholar

5 This method for interpreting the quantifiers was suggested by the referee.

6 If Γ Ε is provable then (α1)(α2) … (αm)(Γ Ε) is provable where α1 ,α2, … αm is a complete list of the free variables in Γ and Ε. We will assume that wherever B1 follows by substitution, the variables in Γ and Ε have been generalized upon.

7 A slightly stronger theorem than XXIX* could be proved as an immediate corollary of XXVIII* if we introduced the following lemma: If ├ A ⊃ B then ├ □ ⊃ □B We would then need only to assume that ├ An □Γ1 where i < n. This alternative proof was suggested by the referee.