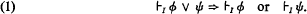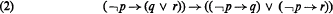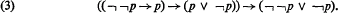Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gabbay, D.M.
1973.
Proceedings of the Fourth International Congress for Logic, Methodology and Philosophy of Science, Bucharest, 1971.
Vol. 74,
Issue. ,
p.
29.
Gabbay, Dov M.
1975.
Decidability results in non-classical logics.
Annals of Mathematical Logic,
Vol. 8,
Issue. 3,
p.
237.
Wolf, Robert G.
1977.
Modern Uses of Multiple-Valued Logic.
p.
167.
Szatkowski, Miros>law
1981.
On fragments of Medvedev's logic.
Studia Logica,
Vol. 40,
Issue. 1,
p.
39.
Minari, Pierluigi
1986.
On the extension of intuitionistic propositional logic with Kreisel-Putnam's and Scott's schemes.
Studia Logica,
Vol. 45,
Issue. 1,
p.
55.
Van Dalen, Dirk
1986.
Handbook of Philosophical Logic.
p.
225.
Shehtman, Valentin
1990.
Modal counterparts of Medvedev logic of finite problems are not finitely axiomatizable.
Studia Logica,
Vol. 49,
Issue. 3,
p.
365.
Chagrov, Alexander
and
Zakharyashchev, Michael
1991.
The disjunction property of intermediate propositional logics.
Studia Logica,
Vol. 50,
Issue. 2,
p.
189.
Miglioli, Pierangelo
1992.
An infinite class of maximal intermediate propositional logics with the disjunction property.
Archive for Mathematical Logic,
Vol. 31,
Issue. 6,
p.
415.
Ferrari, Mauro
and
Miglioli, Pierangelo
1995.
A method to single out maximal propositional logics with the disjunction property I.
Annals of Pure and Applied Logic,
Vol. 76,
Issue. 1,
p.
1.
Ferrari, Mauro
and
Miglioli, Pierangelo
1995.
A method to single out maximal propositional logics with the disjunction property II.
Annals of Pure and Applied Logic,
Vol. 76,
Issue. 2,
p.
117.
Avellone, Alessandro
Fiorentini, Camillo
Mantovani, Paolo
and
Miglioli, Pierangelo
1996.
On maximal intermediate predicate constructive logics.
Studia Logica,
Vol. 57,
Issue. 2-3,
p.
373.
Avellone, Alessandro
Moscato, Ugo
Miglioli, Pierangelo
and
Ornaghi, Mario
1997.
Automated Reasoning with Analytic Tableaux and Related Methods.
Vol. 1227,
Issue. ,
p.
43.
Ohlbach, Hans Jürgen
and
Reyle, Uwe
1999.
Logic, Language and Reasoning.
Vol. 5,
Issue. ,
p.
13.
Zakharyaschev, M.
Wolter, F.
and
Chagrov, A.
2001.
Handbook of Philosophical Logic.
p.
83.
van Dalen, Dirk
2002.
Handbook of Philosophical Logic.
p.
1.
Wolter, Frank
and
Zakharyaschev, Michael
2007.
Handbook of Modal Logic.
Vol. 3,
Issue. ,
p.
427.
Rybakov, Mikhail
2008.
Complexity of intuitionistic propositional logic and its fragments.
Journal of Applied Non-Classical Logics,
Vol. 18,
Issue. 2-3,
p.
267.
Cook, Roy T.
2014.
Should Anti-Realists be Anti-Realists About Anti-Realism?.
Erkenntnis,
Vol. 79,
Issue. S2,
p.
233.
Hamkins, Joel David
Leibman, George
and
Löwe, Benedikt
2015.
Structural connections between a forcing class and its modal logic.
Israel Journal of Mathematics,
Vol. 207,
Issue. 2,
p.
617.