Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-29T17:57:39.404Z Has data issue: false hasContentIssue false
  • English
  • Français

Core models with more Woodin cardinals

Published online by Cambridge University Press:  12 March 2014

J. R. Steel
J. R. Steel*
Affiliation:
Department of Mathematics, The University of California, 717 Evans Hall # 3840, Berkeley. CA 94720-3840, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper, we shall prove two theorems involving the construction of core models with infinitely many Woodin cardinals. We assume familiarity with [12], which develops core model theory the one Woodin level, and with [10] and [6], which extend the fine structure theory of [5] to mice having many Woodin cardinals. The most important new problem of a general nature which we must face here concerns the iterability of Kc with respect to uncountable iteration trees.

Our first result is the following theorem, a slightly stronger version of which was proved independently and earlier by Woodin. The theorem settles positively a conjecture of Feng, Magidor, and Woodin [2].

Theorem. Let Ω be measurable. Then the following are equivalent:

(a) for all posets,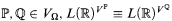

(b) for every poset,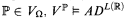

(c) for every poset ℙ ∈ VΩ, Vℙ ⊨ there is no uncountable sequence of distinct reals in L(ℝ)

(d) there is an Ω-iterable premouse of height Ω which satisfies “there are infinitely many Woodin cardinals”.

It is an immediate corollary that if every set of reals in L(ℝ) is weakly homogeneous, then ADL(ℝ) holds. We shall also indicate some extensions of the theorem to pointclasses beyond L(ℝ), and mice with more than ω Woodin cardinals.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 3 , September 2002 , pp. 1197 - 1226
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Andretta, A., Neeman, I., and Steel, J. R., The domestic levels of Kc are iterable, Israel Journal of Mathematics, (to appear).Google Scholar
[2]Feng, Q., Magidor, M., and Woodin, W. H., Universally Baire sets.Google Scholar
[3]Martin, D. A. and Steel, J. R., Iteration trees, Journal American Mathematical Society, vol. 7 (1994), pp. 1–73.CrossRefGoogle Scholar
[4]Mitchell, W. J., Schimmerling, E., and Steel, J. R., The weak covering lemma up to a Woodin cardinal, Annals of Pure and Applied Logic, vol. 84 (1997), pp. 219–255.CrossRefGoogle Scholar
[5]Mitchell, W. J. and Steel, J. R., Fine structure and iteration trees, Lecture Notes in Logic, no. 3, Springer-Verlag, Berlin, 1994.CrossRefGoogle Scholar
[6]Neeman, I. and Steel, J. R., A weak Dodd-Jensen lemma, this Journal, vol. 64 (1999), pp. 1285–1294.Google Scholar
[7]Schimmerling, E. and Steel, J. R., Fine structure for tame inner models, this Journal, vol. 61 (1996), pp. 621–639.Google Scholar
[8]Schimmerling, E. and Steel, J. R., The maximality of the core model, Transactions of the American Mathematical Society, vol. 351 (1999), pp. 3119–3141.CrossRefGoogle Scholar
[9]Schindler, R. D., Steel, J. R., and Zeman, M., Deconstructing inner model theory, (to appear).Google Scholar
[10]Steel, J. R., Inner models with many Woodin cardinals, Annals of Pure and Applied Logic, vol. 65 (1993), pp. 185–209.CrossRefGoogle Scholar
[11]Steel, J. R., The wellfoundedness of the Mitchell order, this Journal, vol. 58 (1993), pp. 931–940.Google Scholar
[12]Steel, J. R., The core model iterability problem, Lecture Notes in Logic, no. 8, Springer-Verlag, Berlin, 1996.CrossRefGoogle Scholar
[13]Steel, J. R., An outline of inner model theory, Handbook of set theory, to appear.Google Scholar