Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T00:17:30.119Z Has data issue: false hasContentIssue false
  • English
  • Français

COPYING ONE OF A PAIR OF STRUCTURES

Part of: Computability and recursion theory

Published online by Cambridge University Press:  29 October 2021

RACHAEL ALVIR ,
HANNAH BURCHFIELD  and
JULIA F. KNIGHT
RACHAEL ALVIR
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NOTRE DAME 255 HURLEY HALL, NOTRE DAME, IN 46556, USA E-mail:[email protected]:[email protected]:[email protected]
HANNAH BURCHFIELD
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NOTRE DAME 255 HURLEY HALL, NOTRE DAME, IN 46556, USA E-mail:[email protected]:[email protected]:[email protected]
JULIA F. KNIGHT
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NOTRE DAME 255 HURLEY HALL, NOTRE DAME, IN 46556, USA E-mail:[email protected]:[email protected]:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

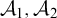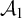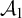We ask when, for a pair of structures $\mathcal {A}_1,\mathcal {A}_2$ , there is a uniform effective procedure that, given copies of the two structures, unlabeled, always produces a copy of $\mathcal {A}_1$ . We give some conditions guaranteeing that there is such a procedure. The conditions might suggest that for the pair of orderings $\mathcal {A}_1$ of type 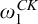$\omega _1^{CK}$ and 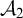$\mathcal {A}_2$ of Harrison type, there should not be any such procedure, but, in fact, there is one. We construct an example for which there is no such procedure. The construction involves forcing. On the way to constructing our example, we prove a general result on modifying Cohen generics.

Keywords

Turing operatorCohen genericgeneric enumeration of family

MSC classification

Primary: 03D99: None of the above, but in this section
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 3 , September 2022 , pp. 1201 - 1214
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ash, C. J. and Knight, J. F., Computable Structures and the Hyperarithmetical Hierarchy, Elsevier, Amsterdam, 2000.Google Scholar
Ash, C. J. and Knight, J. F., Pairs of recursive structures . Annals of Pure and Applied Logic, vol. 46 (1990), pp. 211–234.CrossRefGoogle Scholar
Calvert, W., Frolov, A., Harizanov, V., Knight, J., McCoy, C., Soskova, A., and Vatev, S., Strong jump inversion . Journal of Logic and Computation, vol. 28 (2018), pp. 1499–1522.CrossRefGoogle Scholar
Cohen, P. J., Set Theory and the Continuum Hypothesis, W. A. Benjamin, Inc., 1966, pp. 136–138.Google Scholar
Downey, R. and Jockusch, C., Every low Boolean algebra is isomorphic to a recursive one . PAMS, vol. 122 (1994), pp. 871–880.CrossRefGoogle Scholar
Hirschfeldt, D., Khoussainov, B., Shore, R., and Slinko, A., Degree spectra and computable dimensions in algebraic structures . Annals of Pure and Applied Logic, vol. 115 (2002), pp. 71–113.CrossRefGoogle Scholar
Kalimullin, I., Algorithmic reducibilities of algebraic structures . Journal of Logic and Computation, vol. 22 (2012), pp. 831–843.CrossRefGoogle Scholar
Lachlan, A. H. and Soare, R. I., Models of arithmetic and upper bounds for arithmetic sets , this Journal, vol. 59 (1994), pp. 977–983.Google Scholar
Lachlan, A. H. and Soare, R. I., Models of arithmetic and subuniform bounds for the arithmetic sets , this Journal, vol. 63 (1998), pp. 59–72.Google Scholar
Marker, D. and Miller, R., Turing degree spectra of differentially closed fields , this Journal, vol. 82 (2017), pp. 1–25.Google Scholar
Miller, R. G., Poonen, B., Schoutens, H., and Shlapentokh, A., A computable functor from graphs to fields , this Journal, vol. 83 (2018), pp. 326–348.Google Scholar
Montalban, A., Computable Structure Theory: Within the Arithmetic, Association for Symbolic Logic Perspectives in Logic, Cambridge University Press, 2021.Google Scholar
Rogers, H., Theory of Recursive Functions and Effective Computability, McGraw-Hill, 1967.Google Scholar