Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-16T19:22:26.977Z Has data issue: false hasContentIssue false
  • English
  • Français

A continuous functional with noncollapsing hierarchy

Published online by Cambridge University Press:  12 March 2014

Dag Normann
Dag Normann*
Affiliation:
University of Oslo, Blindern, Oslo-3, Norway
Get access Rights & Permissions [Opens in a new window]

Extract

In [5] S. S. Wainer introduces a hierarchy for arbitrary type-2-functionals. Given F, he defines a set of ordinal notations OF, and for each a ∈ OF, a function fa recursive in F and an ordinal ∣a∣F < 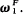For any f recursive in F there is an a ∈ OF such that f is primitive recursive in fa.

Let ρF be the least ordinal α such that for any f recursive in F there is an α ∈ OF with ∣a∣F ≤ α such that f is primitive recursive in fa. If ρF < 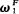the hierarchy breaks down. In Bergstra and Wainer [2] ρF is described as “the real ordinal of the 1-section of F”.

Using standard methods (originally due to Kleene) one may prove that if F is normal, then ρF = 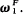Feferman has proved that if F is recursive, then ρF = ω2.

Let 1-section (F) = l-sc(F) = {f; f is recursive in F} where f is a total object of type 1.

Grilliot [4] proved that F ↾ 1-sc(F) is continuous if and only if F is not normal.

Let h be an associate for a given functional F, and assume that h is recursive in the jump of an element of 1-sc(F).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 43 , Issue 3 , September 1978 , pp. 487 - 491
Copyright
Copyright © Association for Symbolic Logic 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bergstra, J., Computability and continuity in finite types, Dissertation, Utrecht, 1976.Google Scholar
[2]Bergstra, J. and Wainer, S., The “real” ordinal of the 1-section of a continuous functional, abstract, this Journal, vol. 42 (1977), p. 440.Google Scholar
[3]Gandy, R. O., Proof of Mostowski's conjecture, Bulletin de l'Académie Polonaise des Sciences, vol. 9 (1960), pp. 571–575.Google Scholar
[4]Grilliot, T., On effectively discontinuous type-2 objects, this Journal, vol. 36 (1971), pp. 245–248.Google Scholar
[5]Wainer, S. S., A hierarchy for the 1-section of any type two object, this Journal, vol. 39 (1974), pp. 88–94.Google Scholar
[6]Sacks, G. E., Degrees of unsolvability, Annals of mathematics studies, Princeton, 1963, 2nd edition, 1966.Google Scholar