T. Jech [4] and M. Takahashi [7] proved that given any partial ordering R in a model 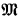of ZFC there is a symmetric submodel of a generic extension of 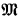where R is isomorphic to the injective ordering on a set of cardinals.

The authors raised the question whether the injective ordering of cardinals can be universal, i.e. whether the following axiom of “cardinal universality” is consistent:

CU. For any partially ordered set (X, ≼) there is a bijection f:X → Y such that

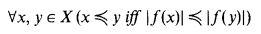
(i.e. x ≼ y iff ∃g: f(x) → f(y) injective). (See [1].)

The consistency of CU relative to ZF0 (Zermelo-Fraenkel set theory without foundation) is proved in [2], but the transfer method of Jech-Sochor-Pincus cannot be applied to obtain consistency with full ZF (including foundation), since CU apparently is not boundable.

In this paper the authors define a model 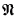of ZF + CU as a symmetric submodel of a generic extension obtained by forcing “à la Easton” with a class of conditions which add κ generic subsets to any regular cardinal κ of a ground model satisfying ZF + V = L.