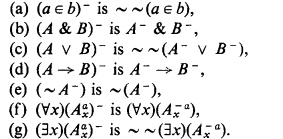Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bernini, Sergio
1976.
Interpretazione intuizionista di teorie a logica classica; una particolare applicazione del metodo della traduzione negativa via concetti empirici e anomici (Lawless).
ANNALI DELL UNIVERSITA DI FERRARA,
Vol. 22,
Issue. 1,
p.
21.
Parsons, Charles
1977.
Logic, Foundations of Mathematics, and Computability Theory.
p.
335.
Friedman, Harvey
1978.
Higher Set Theory.
Vol. 669,
Issue. ,
p.
21.
Hahanyan, V. H.
1981.
The consistency of some intuitionistic and constructive principles with a set theory.
Studia Logica,
Vol. 40,
Issue. 3,
p.
237.
Gordeev, L. N.
1981.
An approach to the constructivization of Cantor's set theory.
Journal of Soviet Mathematics,
Vol. 15,
Issue. 1,
p.
22.
Creenleaf, Newcomb
1981.
Constructive Mathematics.
Vol. 873,
Issue. ,
p.
213.
Goondeev, Lev
1982.
The L. E. J. Brouwer Centenary Symposium, Proceedings of the Conference held in Noordwijkerhout.
Vol. 110,
Issue. ,
p.
123.
Friedman, Harvey
and
Ščedrov, Andrej
1984.
Large sets in intuitionistic set theory.
Annals of Pure and Applied Logic,
Vol. 27,
Issue. 1,
p.
1.
Friedman, Harvey M
and
Ščedrov, Andrej
1985.
The lack of definable witnesses and provably recursive functions in intuitionistic set theories.
Advances in Mathematics,
Vol. 57,
Issue. 1,
p.
1.
Scedrov, Andrej
1985.
Harvey Friedman's Research on the Foundations of Mathematics.
Vol. 117,
Issue. ,
p.
257.
Friedman, Harvey M
and
S̆čedrov, Andrej
1985.
Arithmetic transfinite induction and recursive well-orderings.
Advances in Mathematics,
Vol. 56,
Issue. 3,
p.
283.
Leivant, Daniel
1985.
Harvey Friedman's Research on the Foundations of Mathematics.
Vol. 117,
Issue. ,
p.
231.
Nerode, Anil
and
Harrington, Leo A.
1985.
Harvey Friedman's Research on the Foundations of Mathematics.
Vol. 117,
Issue. ,
p.
1.
Scedrov, Andre
1987.
Logic Colloquium '85.
Vol. 122,
Issue. ,
p.
281.
Beeson, Michael J.
1988.
Towards a computation system based on set theory.
Theoretical Computer Science,
Vol. 60,
Issue. 3,
p.
297.
Khakhanyan, V. Kh.
1988.
Nondeducibility of the uniformization principles from Church's thesis in intuitionistic set theory.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 43,
Issue. 5,
p.
394.
Kashapova, F. R.
1989.
Intuitionistic theory of functionals of a high type.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 45,
Issue. 3,
p.
228.
Simpson, A.K.
1999.
Elementary axioms for categories of classes.
p.
77.
Krivine, J.-L.
2000.
The curry-howard correspondence in set theory.
p.
307.
Aczel, Peter
and
Gambino, Nicola
2002.
Types for Proofs and Programs.
Vol. 2277,
Issue. ,
p.
1.