Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T05:33:55.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Congruence relations on lattices of recursively enumerable sets

Published online by Cambridge University Press:  12 March 2014

Todd Hammond
Todd Hammond*
Affiliation:
Division of Mathematics and Computer Science, Truman State University, Kirksville, MO 63501. USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Let {We}e∈ω be a standard enumeration of the recursively enumerable (r. e.) subsets of ω = {0, 1, 2, …}. The lattice of recursively enumerable sets, 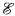is the structure ({We}e∈ω, ∪, ∩). 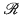is the sublattice of 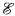consisting of the recursive sets.

Suppose 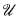is a lattice of subsets of ω. ≡ is said to be a congruence relation on 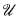if ≡ is an equivalence relation on 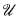and if for all U, U′ ∈ 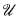and V, V ∈ 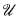, if U ≡ U′ and V ≡ V′ then U ∪ U′ ≡ V ∪ V′ and U ∩ U′ ≡ V ∩ V′. [U] = {V ∈ 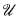| V ≡ U} is the equivalence class of U. If ≡ is a congruence relation on 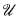, the elements of the quotient lattice 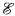/ ≡ are the equivalence classes of ≡. [U] ∪ [V] is defined as [U ∪ V], and [U] ∩ [V] is defined as [U ∩ V].

The quotient lattices of 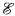(or of some sublattice 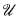) correspond naturally with the congruence relations which give rise to them, and in turn the congruence relations of sublattices of 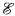can be characterized in part by their computational complexity. The aim of the present paper is to characterize congruence relations in some of the most important complexity classes.

Keywords

recursively enumerablecomputably enumerablecongruence relationidealquotientlattice
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 2 , June 2002 , pp. 497 - 504
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bennison, V. L. and Soare, R. I., Some lowness properties and computational complexity sequences, Theoretical Computer Science, vol. 6 (1978), pp. 233–254.CrossRefGoogle Scholar
[2]Degtev, A. N., Decidability of the ∀∃-theory of a certain factor-lattice of recursively enumerable sets, Algebra i Logika, vol. 17 (1978), pp. 134–143, 241, in Russian: Algebra anil Logic vol. 17 (1978), pp. 94–101, English translation.Google Scholar
[3]Friedberg, R. M., Three theorems on recursive enumeration: I. Decomposition, II. Maximal set, III. Enumeration without duplication, this Journal, vol. 23 (1958), pp. 309–316.Google Scholar
[4]Hammond, T., Friedberg splittings in Σ30 congruence lattices E, in preparation.Google Scholar
[5]Hammond, T., Nonisomorphism of lattices of recursively enumerable sets, this Journal, vol. 58 (1993), pp. 1177–1188.Google Scholar
[6]Harrington, L., The lattice of r. e. sets is undecidable (again), handwritten notes, 1983.Google Scholar
[7]Harrington, L., Lachlan, A. H., Maass, W., and Soare, R. I., Algebraic properties of low2 computable sets, in preparation.Google Scholar
[8]Maass, W., Characterization of recursively enumerable sets with supersets effectively isomorphic to all recursively enumerable sets, Transactions of the American Mathematical Society, vol. 279 (1983), pp. 311–336.CrossRefGoogle Scholar
[9]Morley, M. D. and Soare, R. I., Boolean algebras, splitting theorems and Δ20 sets, Fundamenta Mathematicae, vol. 90 (1975), pp. 45–52.CrossRefGoogle Scholar
[10]Owings, J. C., Recursion, metarecursion, and inclusion, this Journal, vol. 32 (1967), pp. 173–178.Google Scholar
[11]Robinson, R. W., The inclusion lattice and degrees of unsolvability of the recursively enumerable sets, Cornell University, 1966.Google Scholar
[12]Soare, R. I., Automorphisms of the lattice of recursively enumerable sets, Part II: Low sets, Annals of Mathematical Logic, vol. 22 (1982), pp. 69–107.CrossRefGoogle Scholar
[13]Soare, R. I., Recursively enumerable sets and degrees: A study of computable functions and computably generated sets, Springer-Verlag, Heidelberg, 1987.CrossRefGoogle Scholar