Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-22T06:16:31.201Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPUTABILITY AND UNCOUNTABLE LINEAR ORDERS I: COMPUTABLE CATEGORICITY

Published online by Cambridge University Press:  13 March 2015

NOAM GREENBERG ,
ASHER M. KACH ,
STEFFEN LEMPP  and
DANIEL D. TURETSKY
NOAM GREENBERG
Affiliation:
DEPARTMENT OF MATHEMATICS, VICTORIA UNIVERSITY OF WELLINGTON, WELLINGTON, NEW ZEALANDE-mail: [email protected]: http://homepages.mcs.vuw.ac.nz/∼greenberg/
ASHER M. KACH
Affiliation:
DEPARTMENT OF MATHEMATICS, UNIVERSITY OF CONNECTICUT-STORRS, STORRS, CT 06269-3009, USAE-mail: [email protected]: http://www.math.uconn.edu/∼kach/
STEFFEN LEMPP
Affiliation:
DEPARTMENT OF MATHEMATICS, UNIVERSITY OF WISCONSIN, MADISON, WI 53706-1388, USAE-mail: [email protected]: http://www.math.wisc.edu/∼lempp/
DANIEL D. TURETSKY
Affiliation:
KURT GÖDEL RESEARCH CENTER, UNIVERSITY OF VIENNA, VIENNA, AUSTRIAE-mail: [email protected]: http://tinyurl.com/dturetsky
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the computable structure theory of linear orders of size 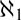$\aleph _1 $ within the framework of admissible computability theory. In particular, we characterize which of these linear orders are computably categorical.

Keywords

Primary: 03D60secondary: 03C57uncountable linear orderscomputabilitycomputable categoricity
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 1 , March 2015 , pp. 116 - 144
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Downey, Rodney G., Computability theory and linear orderings. In Handbook of recursive mathematics, Vol. 2, Studies in Logic and the Foundations of Mathematics, vol. 139 pages 823–976. North-Holland, Amsterdam, 1998.Google Scholar
Ben, Dushnik and Miller, E. W., Concerning similarity transformations of linearly ordered sets. Bulletin of American Mathematical Society, vol. 46 (1940), pp. 322–326.Google Scholar
Dzgoev, Valeri D., On constructivizations of some structures. Akad. Nauk SSSR, Sibirsk. Otdel., Novosibirsk, 1978. manuscript deposited at VINITI on July 26, 1978, Deposition No. 1606–79.Google Scholar
Goncharov, Sergey S. and Dzgoev, Valeri D., Autostability of models. Algebra i Logika, vol. 19 (1980), no. 1, pp. 45–58, 132.Google Scholar
Greenberg, Noam, The role of true finiteness in the admissible recursively enumerable degrees. Memoirs of the American Mathematical Society, 181(854):vi+99, 2006.CrossRefGoogle Scholar
Greenberg, Noam, Kach, Asher M., Lempp, Steffen and Turetsky, Daniel D., Computability and uncountable linear orders, part II: degree spectra, this Journal, accepted.Google Scholar
Greenberg, Noam and Knight, Julia F.. Computable structure theory using admissible recursion theory on ω 1, Effective mathematics of the uncountable (Greenberg, Hirschfeldt, Miller, Hamkins, editors), Lecture Notes in Logic, Association for Symbolic Logic and Cambridge University Press, pp. 50–80, 2013, available at http://www.cambridge.org/nz/academic/subjects/mathematics/logic-categories-and-sets/effective-mathematics-uncountable.Google Scholar
Kreisel, Georg, Set theoretic problems suggested by the notion of potential totality. Infinitistic Methods (Proc. Sympos. Foundations of Math., Warsaw, 1959), pp. 103–140, Pergamon, Oxford, 1961.Google Scholar
Kreisel, Georg and Sacks, Gerald E.. Metarecursive sets I, II (abstracts), this Journal, vol. 28 (1963), pp. 304–305.Google Scholar
Kreisel, Georg, Metarecursive sets, this Journal, vol. 30 (1965), pp. 318–338.Google Scholar
Kripke, Saul A., Transfinite recursion on admissible ordinals I, II (abstracts), this Journal, vol. 29 (1964), pp. 161–162.Google Scholar
Lerman, Manuel, Maximal α-r.e. sets. Transactions of the American Mathematical Society, vol. 188 (1974), pp. 341–386.Google Scholar
Lerman, Manuel and Simpson, Stephen G., Maximal sets in α-recursion theory. Israel Journal of Mathematics, vol. 14 (1973), pp. 236–247.Google Scholar
Platek, Richard A., Foundations of recursion theory, Ph.D. thesis, Stanford Univeristy, Stanford, CA, 1965.Google Scholar
Remmel, Jeffrey B., Recursively categorical linear orderings. Proceedings of the American Mathematical Society, vol. 83 (1981), no. 2, pp. 387–391.Google Scholar
Richter, Linda Jean, Degrees of structures, this Journal, vol. 46 (1981), no. 4, pp. 723–731.Google Scholar
Rosenstein, Joseph G., Linear orderings, Pure and Applied Mathematics, vol. 98, Academic Press Inc. [Harcourt Brace Jovanovich Publishers], New York, 1982.Google Scholar
Sacks, Gerald E., Higher recursion theory, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1990.Google Scholar
Takeuti, Gaisi, On the recursive functions of ordinal numbers. Journal of the Mathematical Society of Japan, vol. 12 (1960), pp. 119–128.Google Scholar
Takeuti, Gaisi, A formalization of the theory of ordinal numbers, this Journal, vol. 30 (1965), pp. 295–317.Google Scholar