No CrossRef data available.
Published online by Cambridge University Press: 01 August 2018
We prove that for every uncountable cardinal κ such that κ<κ = κ, the quasi-order of embeddability on the κ-space of κ-sized graphs Borel reduces to the embeddability on the κ-space of κ-sized torsion-free abelian groups. Then we use the same techniques to prove that the former Borel reduces to the embeddability relation on the κ-space of κ-sized R-modules, for every  $\mathbb{S}$-cotorsion-free ring R of cardinality less than the continuum. As a consequence we get that all the previous are complete
$\mathbb{S}$-cotorsion-free ring R of cardinality less than the continuum. As a consequence we get that all the previous are complete 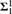 $\Sigma _1^1$ quasi-orders.
$\Sigma _1^1$ quasi-orders.