Published online by Cambridge University Press: 12 March 2014
Here we investigate the classes 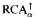 of representable directed cylindric algebras of dimension α introduced by Németi [12].
of representable directed cylindric algebras of dimension α introduced by Németi [12]. 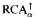 can be seen in two different ways: first, as an algebraic counterpart of higher order logics and second, as a cylindric algebraic analogue of Quasi-Projective Relation Algebras. We will give a new, “purely cylindric algebraic” proof for the following theorems of Németi: (i)
can be seen in two different ways: first, as an algebraic counterpart of higher order logics and second, as a cylindric algebraic analogue of Quasi-Projective Relation Algebras. We will give a new, “purely cylindric algebraic” proof for the following theorems of Németi: (i) 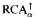 is a finitely axiomatizable variety whenever α ≥ 3 is finite and (ii) one can obtain a strong representation theorem for
is a finitely axiomatizable variety whenever α ≥ 3 is finite and (ii) one can obtain a strong representation theorem for 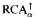 if one chooses an appropriate (non-well-founded) set theory as foundation of mathematics. These results provide a purely cylindric algebraic solution for the Finitization Problem (in the sense of [11]) in some non-well-founded set theories.
if one chooses an appropriate (non-well-founded) set theory as foundation of mathematics. These results provide a purely cylindric algebraic solution for the Finitization Problem (in the sense of [11]) in some non-well-founded set theories.