Article contents
Classifications of generalized index sets of open classes
Published online by Cambridge University Press: 12 March 2014
Extract
The Rice-Shapiro Theorem [4] says that the index set of a class 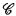 of recursively enumerable (r.e.) sets is r.e. if and only if
of recursively enumerable (r.e.) sets is r.e. if and only if 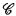 consists of all sets which extend an element of a canonically enumerable sequence of finite sets. If an index of a difference of r.e. (d.r.e.) sets is defined to be the pair of indices of the r.e. sets of which it is the difference, then the following generalization due to Hay [3] is obtained: The index set of a class
consists of all sets which extend an element of a canonically enumerable sequence of finite sets. If an index of a difference of r.e. (d.r.e.) sets is defined to be the pair of indices of the r.e. sets of which it is the difference, then the following generalization due to Hay [3] is obtained: The index set of a class 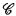 of d.r.e. sets is d.r.e. if and only if
of d.r.e. sets is d.r.e. if and only if 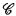 is empty or
is empty or 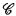 consists of all sets which extend a single fixed finite set. In that paper Hay also classifies index sets of classes consisting of d.r.e. sets which extend one of a finite collection of finite sets. These sets turn out to be finite Boolean combinations of r.e. sets. The question then arises “What about the classification of the index set of a class consisting of d.r.e. sets which extend an element of a canonically enumerable sequence of finite sets?” The results in this paper come from an attempt to answer this question.
consists of all sets which extend a single fixed finite set. In that paper Hay also classifies index sets of classes consisting of d.r.e. sets which extend one of a finite collection of finite sets. These sets turn out to be finite Boolean combinations of r.e. sets. The question then arises “What about the classification of the index set of a class consisting of d.r.e. sets which extend an element of a canonically enumerable sequence of finite sets?” The results in this paper come from an attempt to answer this question.
Since classes of sets which are Boolean combinations of r.e. sets form a hierarchy (the finite Ershov hierarchy, see Ershov [1]) with the r.e. and d.r.e. sets respectively levels 1 and 2 of this hierarchy, we may define index sets of classes of level n sets. If 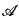 is a class of level n sets which extend some element of a canonically enumerable sequence of finite sets and if we let co-
is a class of level n sets which extend some element of a canonically enumerable sequence of finite sets and if we let co-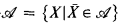 , then we extend the original classification question to the classification of the index sets of the classes
, then we extend the original classification question to the classification of the index sets of the classes 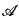 and co-
and co-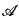 .
.
Now if the sequence of finite sets enumerates only finitely many sets or if only finitely many of the finite sets are minimal under inclusion, then it is a routine computation to verify that the index sets of 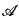 and co-
and co-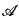 are in the finite Ershov hierarchy. Thus we are interested in the case in which infinitely many of the sequence of finite sets are minimal under inclusion. However if the infinite sequence is fairly simple, for instance{0}, {1}, {2}, … then the r.e. index set of co-
are in the finite Ershov hierarchy. Thus we are interested in the case in which infinitely many of the sequence of finite sets are minimal under inclusion. However if the infinite sequence is fairly simple, for instance{0}, {1}, {2}, … then the r.e. index set of co-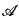 is Σ20-complete as well as the index sets of
is Σ20-complete as well as the index sets of 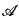 and co-
and co-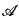 for all levels n > 2. Since the finite Ershov hierarchy does not exhaust ⊿20 there is a lot of “room” between these two extreme cases.
for all levels n > 2. Since the finite Ershov hierarchy does not exhaust ⊿20 there is a lot of “room” between these two extreme cases.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1978
References
REFERENCES
- 1
- Cited by


