Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T05:55:18.988Z Has data issue: false hasContentIssue false
  • English
  • Français

Categoricity transfer in simple finitary abstract elementary classes

Published online by Cambridge University Press:  12 March 2014

Tapani Hyttinen  and
Meeri Kesälä
Tapani Hyttinen
Affiliation:
Department of Mathematics and Statistics, University of Helsinki, P.O. Box 68 (Gustaf Hällströmin Katu 2B), FI-00014 University of Helsinki, Finland, E-mail: [email protected], E-mail: [email protected]
Meeri Kesälä
Affiliation:
Department of Mathematics and Statistics, University of Helsinki, P.O. Box 68 (Gustaf Hällströmin Katu 2B), FI-00014 University of Helsinki, Finland, E-mail: [email protected], E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We continue our study of finitary abstract elementary classes, defined in [7]. In this paper, we prove a categoricity transfer theorem for a case of simple finitary AECs. We introduce the concepts of weak κ-categoricity and f-primary models to the framework of ℵ0-stable simple finitary AECs with the extension property, whereby we gain the following theorem: Let (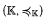) be a simple finitary AEC, weakly categorical in some uncountable κ. Then (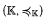) is weakly categorical in each λ ≥ min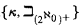. If the class (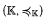) is also 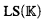-tame, weak κ-categoricity is equivalent with κ-categoricity in the usual sense.

We also discuss the relation between finitary AECs and some other non-elementary frameworks and give several examples.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 76 , Issue 3 , September 2011 , pp. 759 - 806
Copyright
Copyright © Association for Symbolic Logic 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baldwin, John T., Categoricity, University Lecture Series, vol. 50, American Mathematical Society, 2009.Google Scholar
[2]Baldwin, John T. and Kolesnikov, Alexei, Categoricity, amalgamation, and lameness, Israel Journal of Mathematics, vol. 170 (2009), pp. 411–443.CrossRefGoogle Scholar
[3]Grossberg, Rami and VanDieren, Monica, Categoricity from one successor cardinal in tame abstract elementary classes, Journal of Mathematical Logic, vol. 6 (2006), no. 2, pp. 181–201.CrossRefGoogle Scholar
[4]Grossberg, Rami and VanDieren, Monica, Galois-stability in tame abstract elementary classes, Journal of Mathematical Logic, vol. 6 (2006), no. 1, pp. 25–49.CrossRefGoogle Scholar
[5]Grossberg, Rami and VanDieren, Monica, Shelah's categoricity conjecture from a successor for tame abstract elementary classes, this Journal, vol. 71 (2006), no. 2, pp. 553–568.Google Scholar
[6]Hart, Bradd and Shelah, Saharon, Categoricity over P for first order T or categoricity for ψ ∈ 1ω 1ω can stop at ℵk while holding for ℵ0,…, ℵk−1, Israel Journal of Mathematics, vol. 70 (1990), pp. 219–235.Google Scholar
[7]Hyttinen, T. and Kesälä, M., Independence in finitary abstract elementary classes, Annals of Pure and Applied Logic, vol. 143 (2006), no. 1–3, pp. 103–138.CrossRefGoogle Scholar
[8]Hyttinen, Tapani and Kesälä, Meeri, Finitary abstract elementary classes, Ph.D. thesis, University of Helsinki, Department of Mathematics and Statistics, 2006.CrossRefGoogle Scholar
[9]Hyttinen, Tapani and Kesälä, Meeri, Superstability in simple finitary AEC, Fundamenta Mathematicae, vol. 195 (2007), no. 3, pp. 221–268.CrossRefGoogle Scholar
[10]Hyttinen, Tapani and Lessmann, Olivier, A rank for the class of elementary submodels of a superstable homogeneous model, this Journal, vol. 67 (2002), no. 4, pp. 1469–1482.Google Scholar
[11]Hyttinen, Tapani and Lessmann, Olivier, Simplicity and uncountable categoricity in excellent classes, Annals of Pure and Applied Logic, vol. 139 (2006), no. 1–3, pp. 110–137.CrossRefGoogle Scholar
[12]Hyttinen, Tapani, Lessmann, Olivier, and Shelah, Saharon, Interpreting groups and fields in some nonelementary classes, Journal of Mathematical Logic, vol. 5 (2005), no. 1, pp. 1–47.CrossRefGoogle Scholar
[13]Keisler, H. Jerome, Model theory for infinitary logic, Studies in Logic and the Foundations of Mathematics, North-Holland, 1971.Google Scholar
[14]Kueker, David W., Abstract elementary classes and infinitary logics, Annals of Pure and Applied Logic, vol. 156 (2008), no. 2–3, pp. 274–286.CrossRefGoogle Scholar
[15]Laskowski, Michael C., An old friend revisited: countable models of ω-stable theories, Notre Dame Journal of Formal Logic, vol. 48 (2007), no. 1, pp. 133–141.CrossRefGoogle Scholar
[16]Lessmann, Olivier, An introduction to excellent classes, Logic and its applications (Blass, Andreas and Zhang, Yi, editors), Contemporary Mathematics, vol. 380, American Mathematical Society, 2005, pp. 231–259.CrossRefGoogle Scholar
[17]Lessmann, Olivier, An introduction to uncountable categoricity in abstract elementary classes, Graduate Texts in Mathematics, vol. 6, University of Helsinki, Department of Mathematics and Statistics, 2005.Google Scholar
[18]Lessmann, Olivier, Upward categoricity from a successor cardinal for tame abstract classes with amalgamation, this Journal, vol. 70 (2005), no. 2, pp. 639–660.Google Scholar
[19]Shelah, Saharon, Finite diagrams stable in power, Annals of Mathematical Logic, vol. 2 (1970), pp. 293–300.CrossRefGoogle Scholar
[20]Shelah, Saharon, Classification theory and the number of nonisomorphic models, North-Holland, 1978, second revised edition, 1990.Google Scholar
[21]Shelah, Saharon, Classification theory for for nonelementary classes, I. The number of uncountable models of ψ ∈ Lω 1,ω, Parts A and B, Israel Journal of Mathematics, vol. 46 (1983), pp. 212–273.CrossRefGoogle Scholar
[22]Shelah, Saharon, Classification of non elementary classes II, Abstract elementary classes, Classification theory: Proceedings of the V.S.-Israel Workshop on Model Theory in Mathematical Logic, Chicago, 1985 (Baldwin, John T., editor), Lecture Notes in Mathematics, vol. 1292, Springer-Verlag, Berlin, 1987, pp. 419–497.CrossRefGoogle Scholar
[23]Shelah, Saharon, Categoricity of abstract classes with amalgamation, Annals of Pure and Applied Logic, vol. 98 (1999), pp. 261–294.CrossRefGoogle Scholar
[24]Viljanen, Meeri, Independence in local abstract elementary classes, Licantiate's thesis, University of Helsinki, 2005.Google Scholar