Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T09:16:11.434Z Has data issue: false hasContentIssue false
  • English
  • Français

Canonical bases in excellent classes

Published online by Cambridge University Press:  12 March 2014

Tapani Hyttinen  and
Olivier Lessmann
Tapani Hyttinen
Affiliation:
Department of Mathematics and Statistics, P.O. BOX 4, 00014, University of Helsinki, Finland, E-mail: [email protected]
Olivier Lessmann
Affiliation:
Collège Rousseau, Case Postale 216, 1211 Geneva 28, Switzerland, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that any (atomic) excellent class 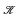can be expanded with hyperimaginaries to form an (atomic) excellent class 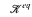which has canonical bases. When 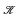is, in addition, of finite U-rank, then 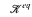is also simple and has a full canonical bases theorem. This positive situation contrasts starkly with homogeneous model theory for example, where the eq-expansion may fail to be homogeneous. However, this paper shows that expanding an ω-stable, homogeneous class 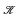gives rise to an excellent class, which is simple if 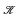is of finite U-rank.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 1 , March 2008 , pp. 165 - 180
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BY]Yaacov, Itay Ben, Discouraging results with ultra-imaginaries, preprint.Google Scholar
[HKP]Hart, Bradd, Kim, Byunghan, and Pillay, Anand, Coordinatisation and canonical bases in simple theories, this Journal, vol. 65 (2000), no. 1, pp. 293–309.Google Scholar
[Hy]Hyttinen, Tapani, Finiteness of U-rank implies simplicity in homogeneous structures, Mathematical Logic Quaterly, vol. 49 (2003), no. 6, pp. 576–578.CrossRefGoogle Scholar
[HyLe]Hyttinen, Tapani and Lessmann, Olivier, Simplicity and uncountable categoricity in excellent classes, Annals of Pure and Applied Logic, vol. 139 (2006), no. 1-3, pp. 110–137.CrossRefGoogle Scholar
[HLS]Hyttinen, Tapani, Lessmann, Olivier, and Shelah, Saharon, Interpreting groups and fields in some nonelementary classes, Journal of Mathematical Logic, vol. 5 (2005), no. 1, pp. 1–47.CrossRefGoogle Scholar
[Le1]Lessmann, Olivier, Categoricity and U-rank in excellent classes, this Journal, vol. 68 (2003), no. 4, pp. 1317–1336.Google Scholar
[Le2]Lessmann, Olivier, An introduction to excellent classes, Logic and its applications, Contemporary Mathematics, vol. 380, AMS, Providence, RI, 231–259 2005.CrossRefGoogle Scholar
[Sh48]Shelah, Saharon, Categoricity in ℵ1 of sentences in Lω1ω (Q), Israel Journal of Mathematics, vol. 20 (1975), pp. 127–148.CrossRefGoogle Scholar
[Sh87a]Shelah, Saharon, Classification theory for nonelementary classes. I. The number of uncountable models of ψ ∈ Lω1ω. Part A, Israel Journal of Mathematics, vol. 46 (1983), pp. 212–240.CrossRefGoogle Scholar
[Sh87b]Shelah, Saharon, Classification theory for nonelementary classes. I. The number of uncountable models of ψ ∈ Lω1ω. Part B, Israel Journal of Mathematics, vol. 46 (1983),pp. 241–273.CrossRefGoogle Scholar
[Zi]Zilber, Boris, Pseudo-exponentiation on algebraically closed fields of characteristic zero, Annals of Pure and Applied Logic, vol. 132 (2005), no. 1, pp. 67–95.CrossRefGoogle Scholar