Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schindler, Ralf
2004.
Semi‐proper forcing, remarkable cardinals, and Bounded Martin's Maximum.
Mathematical Logic Quarterly,
Vol. 50,
Issue. 6,
p.
527.
Asperó, David
2006.
Coding by club-sequences.
Annals of Pure and Applied Logic,
Vol. 142,
Issue. 1-3,
p.
98.
Schindler, Ralf
2006.
Set Theory.
p.
401.
Asperó, David
2009.
On a convenient property about $${[\gamma]^{\aleph_0}}$$.
Archive for Mathematical Logic,
Vol. 48,
Issue. 7,
p.
653.
Bagaria, Joan
2017.
Logic Colloquium '02.
p.
28.
Aspero, David
2017.
Logic Colloquium '02.
p.
1.
Asperó, David
and
Viale, Matteo
2022.
Incompatible bounded category forcing axioms.
Journal of Mathematical Logic,
Vol. 22,
Issue. 02,


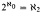 . We also prove that
. We also prove that 