No CrossRef data available.
Article contents
A Boolean ultrapower which is not an ultrapower
Published online by Cambridge University Press: 12 March 2014
Extract
Several people have independently been studying Boolean ultrapowers recently; see for example [2], [3], [4], [6]. Boolean ultrapowers are a quite natural generalization of the well-known usual ultrapowers, but it seemed to be unknown whether every Boolean ultrapower is isomorphic to an ultrapower. We give a negative answer to that question. We further show that a Boolean ultrapower by an ℵ1-regular ultrafilter need not be ℵ2-universal, i.e. that Theorem 4.3.12 of [1] does not hold for Boolean ultrapowers.
Let B be a complete Boolean algebra (we identify the algebra with its underlying set), whose operations are denoted by +, ·, −, 0, 1, Σ, Π Let 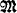 be a structure for some language ℒ.
be a structure for some language ℒ.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1976


