Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T14:05:33.287Z Has data issue: false hasContentIssue false
  • English
  • Français

AXIOMATIZATION OF PROVABLE n-PROVABILITY

Published online by Cambridge University Press:  08 February 2019

EVGENY KOLMAKOV  and
LEV BEKLEMISHEV
EVGENY KOLMAKOV
Affiliation:
STEKLOV MATHEMATICAL INSTITUTE OF RUSSIAN ACADEMY OF SCIENCES 8 GUBKINA STREET, MOSCOW 119991, RUSSIA and FACULTY OF COMPUTER SCIENCE NATIONAL RESEARCH UNIVERSITY HIGHER SCHOOL OF ECONOMICS 3 KOCHNOVSKY PROEZD, MOSCOW 125319, RUSSIAE-mail: [email protected]
LEV BEKLEMISHEV
Affiliation:
STEKLOV MATHEMATICAL INSTITUTE OF RUSSIAN ACADEMY OF SCIENCES 8 GUBKINA STREET, MOSCOW 119991, RUSSIA and FACULTY OF MATHEMATICS NATIONAL RESEARCH UNIVERSITY HIGHER SCHOOL OF ECONOMICS 6 USACHEVA STREET, MOSCOW 119048, RUSSIAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A formula φ is called n-provable in a formal arithmetical theory S if φ is provable in S together with all true arithmetical 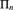${{\rm{\Pi }}_n}$-sentences taken as additional axioms. While in general the set of all n-provable formulas, for a fixed 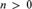$n > 0$, is not recursively enumerable, the set of formulas φ whose n-provability is provable in a given r.e. metatheory T is r.e. This set is deductively closed and will be, in general, an extension of S. We prove that these theories can be naturally axiomatized in terms of progressions of iterated local reflection principles. In particular, the set of provably 1-provable sentences of Peano arithmetic 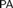$PA$ can be axiomatized by ${\varepsilon _0}$ times iterated local reflection schema over 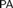$PA$. Our characterizations yield additional information on the proof-theoretic strength of these theories (w.r.t. various measures of it) and on their axiomatizability. We also study the question of speed-up of proofs and show that in some cases a proof of n-provability of a sentence can be much shorter than its proof from iterated reflection principles.

Keywords

03F2503F3003F4003F45strong provability predicatereflection principlePeano arithmeticTuring progressionn-provability
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 2 , June 2019 , pp. 849 - 869
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Beklemishev, L. D., Induction rules, reflection principles, and provably recursive functions. Annals of Pure and Applied Logic, vol. 85 (1997), pp. 193–242.10.1016/S0168-0072(96)00045-0CrossRefGoogle Scholar
Beklemishev, L. D., Parameter free induction and provably total computable functions. Theoretical Computer Science, vol. 224 (1999), no. 1–2, pp. 13–33.10.1016/S0304-3975(98)00305-3CrossRefGoogle Scholar
Beklemishev, L. D., Proof-theoretic analysis by iterated reflection. Archive for Mathematical Logic, vol. 42 (2003), pp. 515–552.10.1007/s00153-002-0158-7CrossRefGoogle Scholar
Beklemishev, L. D., Provability algebras and proof-theoretic ordinals, I. Annals of Pure and Applied Logic, vol. 128 (2004), pp. 103–123.10.1016/j.apal.2003.11.030CrossRefGoogle Scholar
Beklemishev, L. D., Reflection principles and provability algebras in formal arithmetic. Russian Mathematical Surveys, vol. 60 (2005), no. 2, pp. 197–268. Russian original: Uspekhi Matematicheskikh Nauk, vol. 60 (2005), no. 2, pp. 3–78.Google Scholar
Beklemishev, L. D. and Visser, A., On the limit existence principles in elementary arithmetic and ${\rm{\Sigma }}_n^0$-consequences of theories. Annals of Pure and Applied Logic, vol. 136 (2005), no. 1–2, pp. 56–74.10.1016/j.apal.2005.05.005CrossRefGoogle Scholar
Cai, M., Higher unprovability, preprint, 2015.Google Scholar
Feferman, S., Transfinite recursive progressions of axiomatic theories, this Journal, vol. 27 (1962), pp. 259–316.Google Scholar
Goryachev, S. V., On interpretability of some extensions of arithmetic. Mathematical Notes, vol. 40 (1986), no. 5, pp. 821–827. Russian original: Matematicheskie Zametki, vol. 40 (1986), no. 5, pp. 561–572.10.1007/BF01159698CrossRefGoogle Scholar
Ignatiev, K. N., On strong provability predicates and the associated modal logics, this Journal, vol. 58 (1993), pp. 249–290.Google Scholar
Japaridze, G. K., The modal logical means of investigation of provability, Thesis in Philosophy, in Russian, Moscow, 1986.Google Scholar
Japaridze, G. K., The polymodal logic of provability, Intensional Logics and Logical Structure of Theories: Material from the fourth Soviet–Finnish Symposium on Logic, Telavi, May 20–24, 1985, Metsniereba, Tbilisi, 1988, pp. 16–48. In Russian.Google Scholar
Kaye, R., Paris, J.,and Dimitracopoulos, C., On parameter free induction schemas, this Journal, vol. 53 (1988), no. 4, pp. 1082–1097.Google Scholar
Kreisel, G. and Lévy, A., Reflection principles and their use for establishing the complexity of axiomatic systems. Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 14 (1968), pp. 97–142.10.1002/malq.19680140702CrossRefGoogle Scholar
Leivant, D., The optimality of induction as an axiomatization of arithmetic, this Journal, vol. 48 (1983), pp. 182–184.Google Scholar
Ono, H., Reflection principles in fragments of Peano arithmetic. Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 33 (1987), no. 4, pp. 317–333.10.1002/malq.19870330407CrossRefGoogle Scholar
Pudlák, P., On the length of proofs of finitistic consistency statements in first-order theories, Logic Colloquium ’84 (Paris, J. B., Wilkie, A., and Wilmers, J. M., editors), Elsevier, Amsterdam, 1986, pp. 165–196.10.1016/S0049-237X(08)70462-2CrossRefGoogle Scholar
Schmerl, U. R., A fine structure generated by reflection formulas over primitive recursive arithmetic, Logic Colloquium’78 (Boffa, M., van Dalen, D., and McAloon, K., editors), North Holland, Amsterdam, 1979, pp. 335–350.Google Scholar
Smoryński, C., The incompleteness theorems, Handbook of Mathematical Logic (Barwise, J., editor), North Holland, Amsterdam, 1977, pp. 821–865.10.1016/S0049-237X(08)71123-6CrossRefGoogle Scholar
Smoryński, C., Self-Reference and Modal Logic, Springer-Verlag, Berlin, 1985.10.1007/978-1-4613-8601-8CrossRefGoogle Scholar
Turing, A. M., System of logics based on ordinals. Proceedings of the London Mathematical Society, vol. 45 (1939), no. 2, pp. 161–228.10.1112/plms/s2-45.1.161CrossRefGoogle Scholar