Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Leggett, Anne
1974.
Maximal α-R.E. sets and their complements.
Annals of Mathematical Logic,
Vol. 6,
Issue. 3-4,
p.
293.
Lerman, Manuel
1974.
Maximal 𝛼-r.e. sets.
Transactions of the American Mathematical Society,
Vol. 188,
Issue. 0,
p.
341.
Simpson, Stephen G.
1977.
HANDBOOK OF MATHEMATICAL LOGIC.
Vol. 90,
Issue. ,
p.
631.
Soare, Robert I.
1978.
Recursively enumerable sets and degrees.
Bulletin of the American Mathematical Society,
Vol. 84,
Issue. 6,
p.
1149.
Simpson, Stephen G.
1978.
Generalized Recursion Theory II - Proceedings of the 1977 Oslo Symposium.
Vol. 94,
Issue. ,
p.
355.
Odifreddi, Piergiorgio
1981.
Strong reducibilities.
Bulletin of the American Mathematical Society,
Vol. 4,
Issue. 1,
p.
37.
Faust, Don H.
1982.
The Boolean algebra of formulas of first-order logic.
Annals of Mathematical Logic,
Vol. 23,
Issue. 1,
p.
27.
Downey, R.G.
1987.
Maximal theories.
Annals of Pure and Applied Logic,
Vol. 33,
Issue. ,
p.
245.
Downey, Rod
Jockusch, Carl
and
Stob, Michael
1990.
Recursion Theory Week.
Vol. 1432,
Issue. ,
p.
141.
1992.
Vol. 125,
Issue. ,
p.
603.
Cenzer, Douglas
Downey, Rodney
Jockusch, Carl
and
Shore, Richard A.
1993.
Countable thin Π01 classes.
Annals of Pure and Applied Logic,
Vol. 59,
Issue. 2,
p.
79.
Downey, Rod
and
Shore, Richard A.
1996.
Lattice embeddings below a nonlow2 recursively enumerable degree.
Israel Journal of Mathematics,
Vol. 94,
Issue. 1,
p.
221.
Cenzer, Douglas
and
Remmel, Jeffrey
1998.
Index sets for Π01 classes.
Annals of Pure and Applied Logic,
Vol. 93,
Issue. 1-3,
p.
3.
Downey, R.G.
and
Remmel, J.B.
1998.
Handbook of Recursive Mathematics - Volume 2: Recursive Algebra, Analysis and Combinatorics.
Vol. 139,
Issue. ,
p.
977.
Cenzer, D.
and
Remmel, J.B.
1998.
Handbook of Recursive Mathematics - Volume 2: Recursive Algebra, Analysis and Combinatorics.
Vol. 139,
Issue. ,
p.
623.
Ershov, Yu.L.
and
Goncharov, S.S.
1998.
Handbook of Recursive Mathematics - Volume 1: Recursive Model Theory.
Vol. 138,
Issue. ,
p.
115.
Cenzer, Douglas
1999.
Handbook of Computability Theory.
Vol. 140,
Issue. ,
p.
37.
Nies, André
2000.
Effectively dense Boolean algebras and their applications.
Transactions of the American Mathematical Society,
Vol. 352,
Issue. 11,
p.
4989.
Selivanov, Victor
2003.
Computability and Models.
p.
321.
Simpson, Stephen G.
2005.
Mass Problems and Randomness.
Bulletin of Symbolic Logic,
Vol. 11,
Issue. 1,
p.
1.
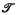 in standard formalization such that all axiomatizable extensions
in standard formalization such that all axiomatizable extensions 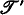 of
of 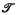 are finite extensions.
are finite extensions.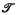 in standard formalization such that
in standard formalization such that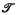 has a consistent, complete, decidable extension
has a consistent, complete, decidable extension 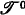 ,
,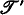 is an axiomatizable extension of
is an axiomatizable extension of 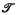 then either
then either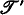 is a finite extension of
is a finite extension of 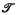 , or
, or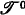 is a finite extension of
is a finite extension of 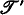 .
.