Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-16T16:58:42.429Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphisms moving all non-algebraic points and an application to NF

Published online by Cambridge University Press:  12 March 2014

Friederike Körner
Friederike Körner*
Affiliation:
Technische Universität Berlin, FB 3 (Mathematik), Strasse des 17. Juni 136. D – 10623 Berlin, Germany E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Section 1 is devoted to the study of countable recursively saturated models with an automorphism moving every non-algebraic point. We show that every countable theory has such a model and exhibit necessary and sufficient conditions for the existence of automorphisms moving all non-algebraic points. Furthermore we show that there are many complete theories with the property that every countable recursively saturated model has such an automorphism.

In Section 2 we apply our main theorem from Section 1 to models of Quine's set theory New Foundations (NF) to answer an old consistency question. If NF is consistent, then it has a model in which the standard natural numbers are a definable subclass ℕ of the model's set of internal natural numbers Nn. In addition, in this model the class of wellfounded sets is exactly .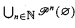

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 63 , Issue 3 , September 1998 , pp. 815 - 830
Copyright
Copyright © Association for Symbolic Logic 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Boffa, M., The consistency problem for NF, this Journal, vol. 42 (1977), pp. 215–220.Google Scholar
[2]Boffa, M. and Pétry, A., On self-membered sets in Quine's set theory NF, Logique et Analyse, vol. 141/142 (1993), pp. 59–60.Google Scholar
[3]Chang, C. C. and Keisler, H. J., Model theory, 3rd ed., North-Holland, 1989.Google Scholar
[4]Forster, T. E., Set theory with a universal set, 2nd ed., Oxford University Press, 1995.CrossRefGoogle Scholar
[5]Hailperin, T., A set of axioms for logic, this Journal, vol. 9 (1944), pp. 1–19.Google Scholar
[6]Henson, C. W., Finite sets in Quine's New Foundations, this Journal, vol. 34 (1969), pp. 589–596.Google Scholar
[7]Hinnion, R., Trois résultats concernant les ensembles fortement cantoriens dans les “New Foundations”, Comptes Rendus de l'Academie des Sciences Paris, Série A, vol. 279 (1974), pp. 41–44.Google Scholar
[8]Kaye, R. W., Models ofPeano arithmetic, Oxford University Press, 1991.CrossRefGoogle Scholar
[9]Kaye, R. W., Kossak, R., and Kotlarski, H., Automorphisms of recursively saturated models of arithmetic, Annals of Pure and Applied Logic, vol. 55 (1991), no. 1, pp. 67–99.CrossRefGoogle Scholar
[10]Kaye, R. W. and Macpherson, D., Models and groups, Automorphisms of first order structures (Kaye, R. W. and Macpherson, H. D., editors), Oxford University Press, 1994, pp. 3–31.CrossRefGoogle Scholar
[11]Körner, F., Cofinal indiscernibles and some applications to New Foundations, Mathematical Logic Quarterly, vol. 40 (1994), pp. 347–356.CrossRefGoogle Scholar
[12]Lascar, D., The small index property and recursively saturated models of Peano arithmetic, Automorphisms of first order structures (Kaye, R. W. and Macpherson, H. D., editors), Oxford University Press, 1994, pp. 281–292.CrossRefGoogle Scholar
[13]Orey, S., New Foundations and the axiom of counting, Duke Mathematical Journal, vol. 31 (1964), pp. 655–660.CrossRefGoogle Scholar
[14]Quine, W. v. O., New Foundations for mathematical logic, American Mathematical Monthly, vol. 44 (1937), pp. 70–80.CrossRefGoogle Scholar
[15]Quine, W. v. O., On ω-inconsistency and a so-called axiom of infinity, this Journal, vol. 18 (1953), pp. 119–124.Google Scholar
[16]Rosser, J. B., Logic for mathematicians, 2nd ed., Chelsea Publishing Company, New York, 1978.Google Scholar
[17]Scott, D. S., Quine's individuals,Proceedings of the 1st international congress for logic, methodology and philosophy of science (Nagel, E., Suppes, P., and Tarski, A., editors), Stanford University Press, Stanford, 1962, pp. 111–115.Google Scholar
[18]Specker, E. P., The axiom of choice in Quine's New Foundations for mathematical logic, Proceedings of the National Academy of Sciences of the United States of America, vol. 39 (1953), pp. 972–975.CrossRefGoogle Scholar