Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T11:31:33.577Z Has data issue: false hasContentIssue false
  • English
  • Français

AROUND RUBIN’S “THEORIES OF LINEAR ORDER”

Part of: Ordered sets Model theory

Published online by Cambridge University Press:  27 October 2020

PREDRAG TANOVIĆ ,
SLAVKO MOCONJA  and
DEJAN ILIĆ
PREDRAG TANOVIĆ
Affiliation:
MATHEMATICAL INSTITUTE SANU KNEZ MIHAILOVA 36, BELGRADE11000, SERBIAE-mail: [email protected]
SLAVKO MOCONJA
Affiliation:
UNIVERSITY OF BELGRADE, FACULTY OF MATHEMATICS STUDENTSKI TRG 16, BELGRADE11000, SERBIA INSTYTUT MATEMATYCZNY, UNIWERSYTET WROCłAWSKI PL. GRUNWALDZKI 2/4, WROCŁAW 50-384, POLANDE-mail: [email protected]
DEJAN ILIĆ
Affiliation:
UNIVERSITY OF BELGRADE, FACULTY OF TRANSPORT AND TRAFFIC ENGINEERING VOJVODE STEPE 305, BELGRADE11000, SERBIAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 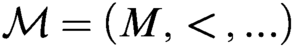$\mathcal M=(M,<,\ldots)$ be a linearly ordered first-order structure and T its complete theory. We investigate conditions for T that could guarantee that $\mathcal M$ is not much more complex than some colored orders (linear orders with added unary predicates). Motivated by Rubin’s work [5], we label three conditions expressing properties of types of T and/or automorphisms of models of T. We prove several results which indicate the “geometric” simplicity of definable sets in models of theories satisfying these conditions. For example, we prove that the strongest condition characterizes, up to definitional equivalence (inter-definability), theories of colored orders expanded by equivalence relations with convex classes.

Keywords

linearly ordered structuresbinary theorieslinear binaritylinear finitenesscolored ordersconvex equivalence relations

MSC classification

Primary: 03C64: Model theory of ordered structures; o-minimality
Secondary: 06A05: Total order
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 4 , December 2020 , pp. 1403 - 1426
Check for updates
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Moconja, S. and Tanović, P., Stationarily ordered types and the number of countable models. Annals of Pure and Applied Logic, vol. 171 (2020), no. 3, p. 102765.CrossRefGoogle Scholar
Poizat, B., A Course in Model Theory: An Introduction to Contemporary Mathematical Logic, Springer Science & Business Media, Berlin, 2012.Google Scholar
Rast, R., The complexity of isomorphism for complete theories of linear orders with unary predicates. Archive for Mathematical Logic, vol. 56 (2017), no. 3-4, pp. 289–307.CrossRefGoogle Scholar
Rosenstein, J. G., Linear Orderings, Academic Press, Cambridge, 1982.Google Scholar
Rubin, M., Theories of linear order. Israel Journal of Mathematics, vol. 17 (1974), no. 4, pp. 392–443.CrossRefGoogle Scholar
Simon, P., On dp-minimal ordered structures, this Journal, vol. 76 (2011), no. 2, pp. 448–460.Google Scholar
Simon, P., A Guide to Nip Theories, Cambridge University Press, Cambridge, 2015.CrossRefGoogle Scholar