Article contents
Approximation theorems and model theoretic forcing
Published online by Cambridge University Press: 12 March 2014
Extract
We suggest the name “approximation theorems” for a new kind of theorems which are strong versions of preservation theorems. A typical preservation theorem has the form:
A sentence φ is preserved by the relation R (i.e. 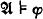 and
and 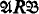 imply
imply 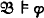 ) iff there exists φ* ϵ Φ such that ⊧φ↔ φ*
) iff there exists φ* ϵ Φ such that ⊧φ↔ φ*
where R is a relation between structures and Φ is a class of sentences (depending, of course, on R). Usually, Φ is described in syntactical terms and it is easy to see that every element of it is, indeed, preserved by R. A typical approximation theorem has the form:
For every sentence Φ there is a sentence Φ* ϵ Φ (the “approximation” of Φ) such that, for all sentences δ which are preserved under R,
(a) if ⊧δ → φ then ⊧δ → φ* and
(b) if ⊧φ → δ then ⊧φ* → δ.
An approximation theorem obviously implies the corresponding preservation theorem.
The first approximation theorem was proved by Vaught in [14] (see Corollary 2.3 below). That paper inspired the present one. Vaught's result is stated in topological terms. It says that for each Borel set B there is an invariant Borel set B* explicitly defined by an L ω1ω sentence, such that B − ⊆ B* ⊆ B + where B − (B +) is the largest (smallest) invariant set included in (containing) B.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1976
References
REFERENCES
- 2
- Cited by


