Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-09T20:33:35.118Z Has data issue: false hasContentIssue false
  • English
  • Français

APPLICATIONS OF PCF THEORY TO THE STUDY OF IDEALS ON

Part of: Set theory

Published online by Cambridge University Press:  11 January 2022

PIERRE MATET
PIERRE MATET*
Affiliation:
UNIVERSITÉ DE CAEN – CNRS LABORATOIRE DE MATHÉMATIQUES BP 5186, 14032CAEN CEDEX, FRANCEE-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 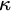$\kappa $ be a regular uncountable cardinal, and 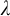a cardinal greater than or equal to 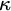$\kappa $ . Revisiting a celebrated result of Shelah, we show that if 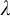is close to 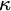$\kappa $ and 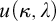(= the least size of a cofinal subset of 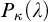) is greater than 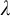, then 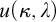can be represented (in the sense of pcf theory) as a pseudopower. This can be used to obtain optimal results concerning the splitting problem. For example we show that if 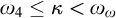and 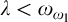, then no 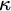$\kappa $ -complete ideal on 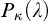is weakly 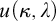-saturated.

Keywords

pcf theorypseudopowerPκ(λ)

MSC classification

Primary: 03E04: Ordered sets and their cofinalities; pcf theory
Secondary: 03E35: Consistency and independence results
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 3 , September 2022 , pp. 967 - 994
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abraham, U. and Magidor, M., Cardinal arithmetic, Handbook of Set Theory, vol. 2 (Foreman, M. and Kanamori, A., eds.), Springer, Berlin, 2010, pp. 1149–1227.CrossRefGoogle Scholar
Donder, H. D. and Matet, P., Two cardinal versions of diamond. Israel Journal of Mathematics, vol. 83 (1993), pp. 1–43.CrossRefGoogle Scholar
Erdös, P., Hajnal, A., Maté, A., and Rado, R., Combinatorial Set Theory: Partition Relations for Cardinals, Studies in Logic and the Foundations of Mathematics, vol. 106, North-Holland, Amsterdam, 1984.Google Scholar
Gitik, M., On gaps under GCH type assumptions. Annals of Pure and Applied Logic, vol. 119 (2003), pp. 1–18.CrossRefGoogle Scholar
Gitik, M. and Shelah, S., On certain indestructibility of strong cardinals and a question of Hajnal. Archive for Mathematical Logic, vol. 28 (1989), pp. 35–42.CrossRefGoogle Scholar
Gitik, M. and Shelah, S., Less saturated ideals. Proceedings of the American Mathematical Society, vol. 125 (1997), pp. 1523–1530.CrossRefGoogle Scholar
Holz, M., Steffens, K., and Weitz, E., Introduction to Cardinal Arithmetic, Birkhäuser Advanced Texts: Basler Lehrbücher, Birkhäuser, Basel, 1999.CrossRefGoogle Scholar
Jech, T., Set Theory, the Third Millenium Edition, Springer Monographs in Mathematics, Springer, Berlin, 2002.Google Scholar
Matet, P., Covering for category and combinatorics on . Journal of the Mathematical Society of Japan, vol. 58 (2006), pp. 153–181.CrossRefGoogle Scholar
Matet, P., Weak square bracket relations for , this Journal, vol. 73 (2008), pp. 729–751.Google Scholar
Matet, P., Game ideals. Annals of Pure and Applied Logic, vol. 158 (2009), pp. 23–39.CrossRefGoogle Scholar
Matet, P., Large cardinals and covering numbers. Fundamenta Mathematicae, vol. 205 (2009), pp. 45–75.CrossRefGoogle Scholar
Matet, P., Weak saturation of ideals on . Mathematical Logic Quarterly, vol. 57 (2011), pp. 149–165.CrossRefGoogle Scholar
Matet, P., Normal restrictions of the non-cofinal ideal on . Fundamenta Mathematicae, vol. 221 (2013), pp. 1–22.CrossRefGoogle Scholar
Matet, P., Two-cardinal diamond star. Mathematical Logic Quarterly, vol. 60 (2014), pp. 246–265.CrossRefGoogle Scholar
Matet, P., Ideals on associated with games of uncountable length. Archive for Mathematical Logic, vol. 54 (2015), pp. 291–328.10.1007/s00153-014-0412-9CrossRefGoogle Scholar
Matet, P., Guessing more sets. Annals of Pure and Applied Logic, vol. 166 (2015), pp. 953–990.10.1016/j.apal.2015.05.001CrossRefGoogle Scholar
Matet, P., Scales with various kinds of good points. Mathematical Logic Quarterly, vol. 64 (2018), pp. 349–370.CrossRefGoogle Scholar
Matet, P., Péan, C., and Shelah, S., Cofinality of normal ideals on II. Israel Journal of Mathematics, vol. 121 (2003), pp. 89–111.Google Scholar
Menas, T. K., On strong compactness and supercompactness. Annals of Mathematical Logic, vol. 7 (1974), pp. 327–359.CrossRefGoogle Scholar
Merimovich, C., Extender-based Radin forcing. Transactions of the American Mathematical Society, vol. 355 (2003), pp. 1729–1772.CrossRefGoogle Scholar
Shelah, S., Around Classification Theory of Models, Lecture Notes in Mathematics, vol. 1182, Springer, Berlin, 1986.CrossRefGoogle Scholar
Shelah, S., Advances in cardinal arithmetic, Finite and Infinite Combinatorics in Sets and Logic (Sands, B., Sauer, N. W., and Woodrow, R. E., editors), NATO ASI series Series C, vol. 411, Kluwer, Dordrecht, 1993, pp. 355–383.10.1007/978-94-011-2080-7_25CrossRefGoogle Scholar
Shelah, S., Cardinal Arithmetic, Oxford Logic Guides, vol. 29, Oxford University Press, Oxford, 1994.Google Scholar
Shelah, S., Further cardinal arithmetic. Israel Journal of Mathematics, vol. 95 (1996), pp. 61–114.10.1007/BF02761035CrossRefGoogle Scholar
Shelah, S., PCF and infinite free subsets in an algebra. Archive for Mathematical Logic, vol. 41 (2002), pp. 321–359.CrossRefGoogle Scholar
Solovay, R., Strongly compact cardinals and the GCH, Proceedings of the Tarski Symposium (Henkin, L. et al., editors), Proc. Sympos. Pure Math., vol. 25, American Mathematical Society, Providence, 1974, pp. 365–372.CrossRefGoogle Scholar
Todorcevic, S., Kurepa families and cofinal similarities, handwritten notes, 1989.Google Scholar
Todorcevic, S., Cofinal Kurepa families, handwritten notes, 1990.Google Scholar
Todorcevic, S., Partitioning pairs of countable sets. Proceedings of the American Mathematical Society, vol. 111 (1991), pp. 841–844.CrossRefGoogle Scholar