Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-17T17:06:54.130Z Has data issue: false hasContentIssue false
  • English
  • Français

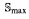An variation for one souslin tree

Published online by Cambridge University Press:  12 March 2014

Paul Larson
Paul Larson*
Affiliation:
Equipe de Logique, Université Paris VII, 2 Place Jussieu, Paris 75251, Cedex, France E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

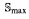We present a variation of the forcing as presented in Woodin [4], Our forcing is a ℙmax-style construction where each model condition selects one Souslin tree. In the extension there is a Souslin tree TG which is the direct limit of the selected Souslin trees in the models of the generic. In some sense, the generic extension is a maximal model of "there exists a minimal Souslin tree,” with TG being this minimal tree. In particular, in the extension this Souslin tree has the property that forcing with it gives a model of Souslin's Hypothesis.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 1 , March 1999 , pp. 81 - 98
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Jech, T., Set theory, Academic Press, 1978.Google Scholar
[2]Shelah, S. and Zapletal, J., Canonical models for ℵ1 combinatorics, in preparation.Google Scholar
[3]Todorčević, S., Trees and linearly ordered sets, Handbook of set-theoretic topology (Kunen, K. and Vaughan, J., editors), North-Holland, 1984, pp. 235–294.Google Scholar
[4]Woodin, W.H., The axiom of determinacy, forcing axioms, and the nonstationary ideal, in preparation.Google Scholar