The problem of treating the semantics of intuitionistic logic within the framework of intuitionistic mathematics was first attacked by E. W. Beth [1]. However, the completeness theorem he thought to have obtained, was not true, as was shown in detail in a report by V. H. Dyson and G. Kreisel [2]. Some vague remarks of Beth's, for instance in his book, The foundations of mathematics , show that he sustained the hope of restoring his proof. But arguments by K. Gödel and G. Kreisel gave people the feeling that an intuitionistic completeness theorem would be impossible [3]. (A (strong) completeness theorem would imply

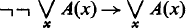
for any primitive recursive predicate A of natural numbers, and one has no reason to believe this for the usual intuitionistic interpretation.) Nevertheless, the following contains a correct intuitionistic completeness theorem for intuitionistic predicate logic. So the old arguments by Godel and Kreisel should not work for the proposed semantical construction of intuitionistic logic. They do not, indeed. The reason is, loosely speaking, that negation is treated positively.

Although Beth's semantical construction for intuitionistic logic was not satisfying from an intuitionistic point of view, it proved to be useful for the development of classical semantics for intuitionistic logic. A related and essentially equivalent classical semantics for intuitionistic logic was found by S. Kripke [4].