Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-25T10:39:15.183Z Has data issue: false hasContentIssue false
  • English
  • Français

An introduction to recursively saturated and resplendent models1

Published online by Cambridge University Press:  12 March 2014

Jon Barwise  and
John Schlipf
Jon Barwise
Affiliation:
University of Wisconsin, Madison, Wisconsin 53706
John Schlipf
Affiliation:
University of Wisconsin, Madison, Wisconsin 53706
Get access Rights & Permissions [Opens in a new window]

Extract

The notions of recursively saturated and resplendent models grew out of the study of admissible sets with urelements and admissible fragments of L ω1ω, but, when applied to ordinary first order model theory, give us new tools for research and exposition. We will discuss their history in §3.

The notion of saturated model has proven to be important in model theory. Its most important property for applications is that if 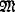, 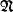are saturated and of the same cardinality then 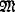= 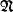iff 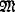≅ 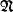. See, e.g., Chang-Keisler [3]. The main drawback is that saturated models exist only under unusual assumptions of set theory. For example, if 2κ = κ+ then every theory T of L has a saturated model of power κ+. (Similarly, if κ is strongly inaccessible, then every T has a saturated model of power κ.) On the other hand, a theory T like Peano arithmetic, with 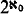types, cannot have a saturated model in any power κ with ω ≤ κ ≤ .

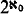One method for circumventing these problems of existence (or rather non-existence) is the use of “special” models (cf. [3]). If κ = Σλ<κ2λ, κ < ω, then every theory T of L has a special model of power κ. Such cardinals are large and, themselves, rather special. There are definite aesthetic objections to the use of these large, singular models to prove results about first order logic.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 41 , Issue 2 , June 1976 , pp. 531 - 536
Copyright
Copyright © Association for Symbolic Logic 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

2

The first author is an Alfred P. Sloan Fellow.

3

Part of the research for this paper was done while the second author held an NSF Graduate Fellowship at the University of Wisconsin.

1

This paper is essentially the text of an invited hour address presented to the Association on April 25,1975 at its spring meeting in Chicago by the first author. Its preparation was supported by NSF grant GP-43882X.

References

REFERENCES

[1] Barwise, J., Admissible sets and structures, “Perspectives in Mathematical Logic” Springer-Verlag, Heidelberg, 1975.CrossRefGoogle Scholar
[2] Barwise, J. and Schlipf, J., Recursively saturated models of Peano arithmetic (to appear).Google Scholar
[3] Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[4] Keisler, H. J., Finite approximations of infinitely long formulas, The theory of models, North-Holland, Amsterdam, 1965, pp. 158–169.Google Scholar
[5] Kleene, S. C., Finite axiomatizability of theories in the predicate calculus using additional predicate symbols. Two papers on the predicate calculus, Memoirs of the American Mathematical Society, no. 10, 1952, pp. 27–68.Google Scholar
[6] Kueker, D., Generalized interpolation and definability, Annals of Mathematical Logic, vol. 1, pp. 423–468.CrossRefGoogle Scholar
[7] Nadel, M., Model theory in admissible sets, Ph.D. Thesis, University of Wisconsin, 1971.Google Scholar
[8] Ressayre, J.-P., Models with compactness properties relative to an admissible language, unpublished notes, 1973.Google Scholar
[9] Schlipf, J., Some hyperelementary aspects of model theory, Ph.D. Thesis, University of Wisconsin, 1975.Google Scholar
[10] Schmerl, J. H., An axiomatization for a class of two-cardinal models (to appear).Google Scholar
[11] Svenonius, L., On the denumerable models of theories with extra predicates, The theory of models, North-Holland, Amsterdam, 1965, pp. 376–389.Google Scholar