Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-17T15:08:16.569Z Has data issue: false hasContentIssue false
  • English
  • Français

An effective selection theorem

Published online by Cambridge University Press:  12 March 2014

Ashok Maitra
Ashok Maitra*
Affiliation:
Indian Statistical Institute, Calcutta 700 035, India
Get access Rights & Permissions [Opens in a new window]

Extract

A recent result of J.P. Burgess [1] states:

Theorem 0. Let F be a multifunction from an analytic subset T of a Polish space to a Polish space X. If F is Borel measurable, Graph(F) is coanalytic in T × X and F(t) is nonmeager in its closure 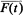for each t Є T, then F admits a Borel measurable selector.

The above result unifies and significantly extends earlier results of H. Sarbadhikari [8], S.M. Srivastava [9] and G. Debs (unpublished). The reader is referred to [1] for details.

The aim of this article is to give an effective version of Theorem 0. We do this by proving a basis theorem for Π11 sets which are nonmeager in their closure and satisfy a local version of the measurability condition in Theorem 0. Our basis theorem generalizes a well-known result of P.G. Hinman [4] and S.K. Thomason [10] (see also [5] and [7, 4F.20]). Our methods are similar to those used by A. Louveau to prove that a 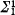, σ-compact set is contained in a , σ-compact set (see [7, 4F.18]).

The paper is organized as follows. §2 is devoted to preliminaries. In §3, we prove the basis theorem and deduce as a consequence an effective version of Theorem 0. We show in §4 how our methods can be used to give alternative proofs of some known results.

Discussions with R. Barua, B.V. Rao and V.V. Srivatsa are gratefully acknowledged. I am indebted to J.P. Burgess for drawing my attention to an error in an earlier draft of this paper.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 47 , Issue 2 , June 1982 , pp. 388 - 394
Copyright
Copyright © Association for Symbolic Logic 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Burgess, J. P., Careful choices: A last word on Borel selectors, preprint, 1979.Google Scholar
[2]Cenzer, D. and Mauldin, R. D., Inductive definability: Measure and category, Advances in Mathematics, vol. 38 (1980), pp. 55–90.CrossRefGoogle Scholar
[3]Hillard, G., Une généralization du théorème de Saint-Raymond sur les boréliens à coupes Kσ, Comptes Rendues Hebdomadaires des Séances de l'Académie des Sciences. Séries A. (Paris), no. 288 (1979), pp. 749–751.Google Scholar
[4]Hinman, P. G., Some applications of forcing to hierarchy problems in arithmetic, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 15 (1969), pp. 341–352.CrossRefGoogle Scholar
[5]Kechris, A. S., Measure and category in effective descriptive set theory, Annals of Mathematical Logic, vol. 5 (1973), pp. 337–384.CrossRefGoogle Scholar
[6]Louveau, A., Recursivity and compactness, Proceedings of the Oberwolf ach Conference, April 1977, Springer-Verlag, Berlin and New York, 1978.Google Scholar
[7]Moschovakis, Y. N., Descriptive set theory, North-Holland, Amsterdam, 1980.Google Scholar
[8]Sarbadhikari, H., Some uniformization results, Fundamenta Mathematicae, vol. 97 (1977), pp. 209–214.CrossRefGoogle Scholar
[9]Srivastava, S. M., Selection theorems for G∂-valued multifunctions, Transactions of the American Mathematical Society, vol. 254 (1979), pp. 283–193.Google Scholar
[10]Thomason, S. K., The forcing method and the upper semi-lattice of hyperdegrees, Transactions of the American Mathematical Society, vol. 129 (1967), pp. 38–57.CrossRefGoogle Scholar
[11]Vaught, R. L., Invariant sets in topology and logic, Fundamenta Mathematicae, vol. 82 (1974), pp. 269–294.CrossRefGoogle Scholar