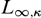We show that for any uncountable cardinal λ, the category of sets of cardinality at least λ and monomorphisms between them cannot appear as the category of points of a topos, in particular is not the category of models of a 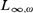${L_{\infty ,\omega }}$-theory. More generally we show that for any regular cardinal 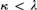$\kappa < \lambda$ it is neither the category of κ-points of a κ-topos, in particular, nor the category of models of a 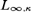${L_{\infty ,\kappa }}$-theory.

The proof relies on the construction of a categorified version of the Scott topology, which constitute a left adjoint to the functor sending any topos to its category of points and the computation of this left adjoint evaluated on the category of sets of cardinality at least λ and monomorphisms between them. The same techniques also apply to a few other categories. At least to the category of vector spaces of with bounded below dimension and the category of algebraic closed fields of fixed characteristic with bounded below transcendence degree.