No CrossRef data available.
Article contents
AMALGAMABLE DIAGRAM SHAPES
Published online by Cambridge University Press: 05 February 2019
Abstract
A category has the amalgamation property (AP) if every pushout diagram has a cocone, and the joint embedding property (JEP) if every finite coproduct diagram has a cocone. We show that for a finitely generated category I, the following are equivalent: (i) every I-shaped diagram in a category with the AP and the JEP has a cocone; (ii) every I-shaped diagram in the category of sets and injections has a cocone; (iii) a certain canonically defined category 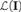 ${\cal L}\left( {\bf{I}} \right)$ of “paths” in I has only idempotent endomorphisms. When I is a finite poset, these are further equivalent to: (iv) every upward-closed subset of I is simply-connected; (v) I can be built inductively via some simple rules. Our proof also shows that these conditions are decidable for finite I.
${\cal L}\left( {\bf{I}} \right)$ of “paths” in I has only idempotent endomorphisms. When I is a finite poset, these are further equivalent to: (iv) every upward-closed subset of I is simply-connected; (v) I can be built inductively via some simple rules. Our proof also shows that these conditions are decidable for finite I.
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019


