Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-06T06:51:16.426Z Has data issue: false hasContentIssue false
  • English
  • Français

THE ADDITIVE GROUPS OF 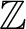$\mathbb {Z}$ AND 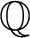$\mathbb {Q}$ WITH PREDICATES FOR BEING SQUARE-FREE

Part of: General logic Model theory

Published online by Cambridge University Press:  05 October 2020

NEER BHARDWAJ  and
CHIEU-MINH TRAN
NEER BHARDWAJ
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGNURBANA, IL61801, USAE-mail: [email protected]
CHIEU-MINH TRAN
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NOTRE DAMENOTRE DAME, IN46556, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

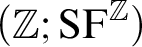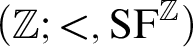We consider the structures $(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$ , $(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$ , 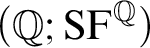$(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$ , and $(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$ where 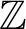$\mathbb {Z}$ is the additive group of integers, 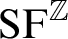$\mathrm {SF}^{\mathbb {Z}}$ is the set of 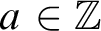$a \in \mathbb {Z}$ such that 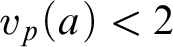$v_{p}(a) < 2$ for  every prime p and corresponding p-adic valuation $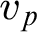v_{p}$ , 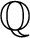$\mathbb {Q}$ and $\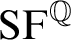mathrm {SF}^{\mathbb {Q}}$ are defined likewise for rational numbers, and $<$ denotes the natural ordering on each of these domains. We prove that the second structure is model-theoretically wild while the other three structures are model-theoretically tame. Moreover, all these results can be seen as examples where number-theoretic randomness yields model-theoretic consequences.

Keywords

model theorydecidabilityneostabilitysquare-free integers

MSC classification

Primary: 03C65: Models of other mathematical theories
Secondary: 03B25: Decidability of theories and sets of sentences 03C10: Quantifier elimination, model completeness and related topics 03C64: Model theory of ordered structures; o-minimality
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 4 , December 2021 , pp. 1324 - 1349
Check for updates
Copyright
© Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, H., Strong theories, burden, and weight, unpublished, 2007.CrossRefGoogle Scholar
Bateman, P.T., Jockusch, C.G., and Woods, A.R., Decidability and undecidability of theories with a predicate for the primes, this Journal, vol. 58 (1993), no. 2, pp. 672–687.Google Scholar
Belegradek, O., Peterzil, Y., and Wagner, F., Quasi-o-minimal structures, this Journal, vol. 65 (2000), no. 3, pp. 1115–1132.Google Scholar
Chernikov, A., Theories without the tree property of the second kind. Annals of Pure and Applied Logic, vol. 165 (2014), no. 2, pp. 695–723.10.1016/j.apal.2013.10.002CrossRefGoogle Scholar
Chernikov, A., Palacin, D., and Takeuchi, K., On $n$ -dependence. Notre Dame Journal of Formal Logic, vol. 60 (2019), no. 2, pp. 195–214.CrossRefGoogle Scholar
Conant, G., There are no intermediate structures between the group of integers and Presburger arithmetic, this Journal, vol. 83 (2018), no. 1, pp. 187–207.Google Scholar
Dolich, A. and Goodrick, J., Strong theories of ordered abelian groups. Fundamenta Mathematicae, vol. 236 (2017), no. 3, pp. 269–296.10.4064/fm256-5-2016CrossRefGoogle Scholar
Gurevich, Y. and Schmitt, P.H., The theory of ordered abelian groups does not have the independence property. Transactions of the American Mathematical Society, vol. 284 (1984), no. 1, pp. 171–182.10.1090/S0002-9947-1984-0742419-0CrossRefGoogle Scholar
Kaplan, I. and Shelah, S., Decidability and classification of the theory of integers with primes, this Journal, vol. 82 (2017), no. 3, pp. 1041–1050.Google Scholar
Kim, B., Simplicity Theory, Oxford Logic Guides, vol. 53, Oxford University Press, Oxford, 2014.Google Scholar
Kim, B., Kim, H.J., and Scow, L., Tree indiscernibilities, revisited. Archive for Mathematical Logic, vol. 53 (2014), no. 1–2, pp. 211–232.10.1007/s00153-013-0363-6CrossRefGoogle Scholar
Mirsky, L., Note on an asymptotic formula connected with $r$ -free integers. The Quarterly Journal of Mathematics Oxford Series, vol. 18 (1947), pp. 178–182.CrossRefGoogle Scholar
Rogers, K., The Schnirelmann density of the squarefree integers. Proceedings of the American Mathematical Society, vol. 15 (1964), pp. 515–516.Google Scholar
Tran, M. C., Tame structures via multiplicative character sums on varieties over finite fields, arXiv preprint, 2017, arXiv:1704.03853.Google Scholar
Wagner, F. O., Stable Groups, London Mathematical Society Lecture Note Series, vol. 240, Cambridge University Press, Cambridge, 1997.10.1017/CBO9780511566080CrossRefGoogle Scholar