Article contents
Π10 classes with complex elements
Published online by Cambridge University Press: 12 March 2014
Abstract
An infinite binary sequence is complex if the Kolmogorov complexity of its initial segments is bounded below by a computable function. We prove that a 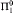 class P contains a complex element if and only if it contains a wtt-cover for the Cantor set. That is, if and only if for every Y ⊆ ω there is an X in P such that X ≥wttY. We show that this is also equivalent to the
class P contains a complex element if and only if it contains a wtt-cover for the Cantor set. That is, if and only if for every Y ⊆ ω there is an X in P such that X ≥wttY. We show that this is also equivalent to the 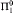 class's being large in some sense. We give an example of how this result can be used in the study of scattered linear orders.
class's being large in some sense. We give an example of how this result can be used in the study of scattered linear orders.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2008
References
REFERENCES
- 7
- Cited by


