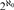Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-22T21:22:24.679Z Has data issue: false hasContentIssue false
  • English
  • Français

${2^{{\aleph _0}}}$ PAIRWISE NONISOMORPHIC MAXIMAL-CLOSED SUBGROUPS OF SYM(ℕ) VIA THE CLASSIFICATION OF THE REDUCTS OF THE HENSON DIGRAPHS

Published online by Cambridge University Press:  01 August 2018

LOVKUSH AGARWAL  and
MICHAEL KOMPATSCHER
LOVKUSH AGARWAL
Affiliation:
SCHOOL OF MATHEMATICS UNIVERSITY OF LEEDS LEEDS, LS2 9JT UKE-mail:[email protected]
MICHAEL KOMPATSCHER
Affiliation:
DEPARTMENT OF ALGEBRA MFF UK SOKOLOVSKA 83 186 00 PRAHA 8 CZECH REPUBLICE-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

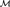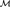Given two structures ${\cal M}$ and ${\cal N}$ on the same domain, we say that ${\cal N}$ is a reduct of ${\cal M}$ if all $\emptyset$-definable relations of ${\cal N}$ are $\emptyset$-definable in 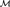${\cal M}$. In this article the reducts of the Henson digraphs are classified. Henson digraphs are homogeneous countable digraphs that omit some set of finite tournaments. As the Henson digraphs are ${\aleph _0}$-categorical, determining their reducts is equivalent to determining the closed supergroups G ≤ Sym(ℕ) of their automorphism groups.

A consequence of the classification is that there are 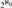${2^{{\aleph _0}}}$ pairwise noninterdefinable Henson digraphs which have no proper nontrivial reducts. Taking their automorphisms groups gives a positive answer to a question of Macpherson that asked if there are ${2^{{\aleph _0}}}$ pairwise nonconjugate maximal-closed subgroups of Sym(ℕ). By the reconstruction results of Rubin, these groups are also nonisomorphic as abstract groups.

Keywords

03C0703C1503C4020B2720B35maximal-closed subgroups of Sym(ℕ)reductsHenson digraphsfirst-order definabilityhomogeneous structurestypesorbitscanonical functions
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 2 , June 2018 , pp. 395 - 415
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Agarwal, L., Reducts of the generic digraph. Annals of Pure and Applied Logic, vol. 167 (2016), pp. 370–391.CrossRefGoogle Scholar
Bodirsky, M., Bradley-Williams, D., Pinsker, M., and Pongrácz, A., The universal homogeneous binary tree. Journal of Logic and Computation, vol. 28 (2018), no. 1, pp. 133–164.CrossRefGoogle Scholar
Bodirsky, M. and Macpherson, D., Reducts of structures and maximal-closed permutation groups, this Journal, vol. 81 (2016), pp. 1087–1114.Google Scholar
Bodirsky, M. and Pinsker, M., Reducts of Ramsey Structures, Contemporary Mathematics: Model Theoretic Methods in Finite Combinatorics, vol. 558 (Grohe, M. and Makowsky, J. A., editors), American Mathematical Society, Providence, RI, 2011, pp. 489–519.CrossRefGoogle Scholar
Bodirsky, M. and Pinsker, M., Canonical functions: A proof via topological dynamics, preprint, 2016, arXiv:1610.09660.Google Scholar
Bodirsky, M., Pinsker, M., and Pongrácz, A., The 42 reducts of the random ordered graph. Proceedings of the London Mathematical Society. Third Series, vol. 111 (2015), no. 3, pp. 591–632.CrossRefGoogle Scholar
Bodirsky, M., Pinsker, M., and Tsankov, T., Decidability of definability, this Journal, vol. 78 (2013), pp. 1036–1054.Google Scholar
Bodor, B., Cameron, P. J., and Szabó, C., Infinitely many reducts of homogeneous structures, preprint, 2016, arXiv:1609.07694.Google Scholar
Bogomolov, F. and Rovinsky, M., Collineation group as a subgroup of the symmetric group. Open Mathematics, vol. 11 (2013), no. 1, pp. 17–26.CrossRefGoogle Scholar
Bossière, F., The countable infinite Boolean vector space and constraint satisfaction problems, Ph.D. thesis, TU Dresden, 2015.Google Scholar
Cameron, P. J., Transitivity of permutation groups on unordered sets. Mathematische Zeitschrift, vol. 148 (1976), pp. 127–139.CrossRefGoogle Scholar
Fraïssé, R., Sur certaines relations généralisent l’ordre des nombres rationnels. Comptes Rendus d’ l’Académie des Sciences de Paris, vol. 237 (1953), pp. 540–542.Google Scholar
Henson, C. W., Countable homogeneous relational structures and ${\aleph _0}$-categorical theories, this Journal, vol. 37 (1972), pp. 494–500.Google Scholar
Hodges, W., A Shorter Model Theory, Cambridge University Press, Cambridge, 1997.Google Scholar
Jasiński, J., Laflamme, C., Nguyen Van Thé, L., and Woodrow, R., Ramsey precompact expansions of homogeneous directed graphs. Electronic Journal of Combinatorics, vol. 21 (2014), no. 4, pp. 1–31.Google Scholar
Junker, M. and Ziegler, M., The 116 reducts of (ℚ,<, 0), this Journal, vol. 74 (2008), pp. 861–884.Google Scholar
Kaplan, I. and Simon, P., The affine and projective groups are maximal. Transactions of the American Mathematical Society, vol. 368 (2016), no. 7, pp. 5229–5245.CrossRefGoogle Scholar
Lachlan, A. H. and Woodrow, R. E., Countable ultrahomogeneous undirected graphs. Transactions of the American Mathematical Society, vol. 262 (1980), pp. 51–94.CrossRefGoogle Scholar
Linman, J. and Pinsker, M., Permutations on the random permutation. Electronic Journal of Combinatorics, vol. 22 (2015), no. 2, pp. 1–22.Google Scholar
Macpherson, D., A survey of homogeneous structures. Discrete Mathematics, vol. 311 (2011), no. 15, pp. 1599–1634.CrossRefGoogle Scholar
Macpherson, D. and Neumann, P. M., Subgroups of infinite symmetric groups. Journal of the London Mathematical Society, vol. 42 (1996), no. 2, pp. 64–84.Google Scholar
Nešetřil, J. and Rödl, V., Ramsey classes of set systems. Journal of Combinatorial Theory (A), vol. 34 (1983), pp. 183–201.CrossRefGoogle Scholar
Pach, P. P., Pinsker, M., Pluhár, G., Pongrácz, A., and Szabó, C., Reducts of the random partial order. Advances in Mathematics, vol. 267 (2014), pp. 94–120.CrossRefGoogle Scholar
Rubin, M., On the reconstruction of ${\aleph _0}$-categorical structures from their automorphism groups. Proceedings of the London Mathematical Society, vol. 69 (1994), no. 3, pp. 225–249.CrossRefGoogle Scholar
Thomas, S., Reducts of the random graph, this Journal, vol. 56 (1991), pp. 176–181.Google Scholar
Thomas, S., Reducts of random hypergraphs. Annals of Pure and Applied Logic, vol. 80 (1996), pp. 165–193.CrossRefGoogle Scholar