Hostname: page-component-6bf8c574d5-pdxrj Total loading time: 0 Render date: 2025-03-11T23:56:56.913Z Has data issue: false hasContentIssue false
  • English
  • Français

A Δ02 theory of regressive isols

Published online by Cambridge University Press:  12 March 2014

Erik Ellentuck
Erik Ellentuck*
Affiliation:
Rutgers, The State University, New Brunswick, New Jersey 08903 Institute for Advanced Study, Princeton, New Jersey 08540
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the action of unary 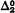functions on the regressive isols. A manageable theory is produced and we find that such a function maps ⋀R into ⋀ if and only if it is eventually R↑ increasing and maps ⋀R into ⋀R if and only if it is eventually recursive increasing. Our paper concludes with a discussion of other methods for extending functions to ⋀R.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 39 , Issue 3 , September 1974 , pp. 459 - 468
Copyright
Copyright © Association for Symbolic Logic 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barback, J., Recursive functions and regressive isols, Mathematica Scandinavica, vol. 15 (1964), pp. 29–42.Google Scholar
[2]Dekker, J. C. E., Infinite series of isols, Proceedings of Symposia in Pure Mathematics, vol. 5, American Mathematical Society, Providence, Rhode Island, 1962, pp. 77–96.Google Scholar
[3]Dekker, J. C. E. and Myhill, J., Retraceable sets, Canadian Journal of Mathematics, vol. 10 (1958), pp. 357–373.CrossRefGoogle Scholar
[4]Myhill, J., Recursive equivalence types and combinatorial functions, Bulletin of the American Mathematical Society, vol. 64 (1958), pp. 373–376.CrossRefGoogle Scholar
[5]Nerode, A., Combinatorial series and recursive equivalence types, Fundamenta Mathematicae, vol. 58 (1966), pp. 113–141.CrossRefGoogle Scholar