Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T04:10:15.621Z Has data issue: false hasContentIssue false
  • English
  • Français

Monte-Carlo techniques for radiotherapy applications I: introduction and overview of the different Monte-Carlo codes

Published online by Cambridge University Press:  27 February 2023

Andrew L. Fielding Open the ORCID record for Andrew L. Fielding [Opens in a new window]
Andrew L. Fielding*
Affiliation:
School of Chemistry and Physics, Queensland University of Technology (QUT), Brisbane, Australia
*
Author for correspondence: Andrew L. Fielding, School of Chemistry and Physics, Queensland University of Technology (QUT), Brisbane, Australia. E-mail [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Introduction:

The dose calculation plays a crucial role in many aspects of contemporary clinical radiotherapy treatment planning process. It therefore goes without saying that the accuracy of the dose calculation is of very high importance. The gold standard for absorbed dose calculation is the Monte-Carlo algorithm.

Methods:

This first of two papers gives an overview of the main openly available and supported codes that have been widely used for radiotherapy simulations.

Results:

The paper aims to provide an overview of Monte-Carlo in the field of radiotherapy and point the reader in the right direction of work that could help them get started or develop their existing understanding and use of Monte-Carlo algorithms in their practice.

Conclusions:

It also serves as a useful companion to a curated collection of papers on Monte-Carlo that have been published in this journal.

Keywords

Monte-Carlo simulationRadiotherapyRadiation Dosimetry
Type
Literature Review
Information
Journal of Radiotherapy in Practice , Volume 22 , 2023 , e80
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution and reproduction, provided the original article is properly cited.
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Introduction

The Monte-Carlo method is a statistical random sampling technique for solving complex multi-dimensional integral equations that are difficult to solve analytically. The general method was introduced in 1949 by Metropolis and Ulam. Reference Metropolis and Ulam1 X-ray interactions at energies of interest in radiotherapy and medical imaging typically result in the production of charged particles such as electrons and positrons. The Boltzmann transport equation can be used to describe the motion of the coupled X-ray and charged particle transport through a defined geometry. Reference Duderstadt and Martin2,Reference do Amaral Rodriguez and Vilhena3 An exact deterministic solution to this complex multi-dimensional equation is difficult to obtain, providing motivation for the use of the more efficient statistical Monte-Carlo method to solve the problem. One of the early demonstrations of the value of the Monte-Carlo method for modelling X-ray interactions was published in 1957 by Bruce and Johns. Reference Bruce and Johns4 They showed how the Monte-Carlo method could be used to calculate the spectra of scattered X-rays in water for a radiotherapy X-ray beam. A solution to the problem of using Monte-Carlo methods for simulating the transport of electrons was proposed in 1963 by Berger, Reference Berger5 introducing the method known as the condensed history technique. Modelling the transport of ionising radiation using Monte-Carlo lends itself to implementation on digital computers, and Berger notes the implementation of his algorithm on an IBM 704 computer in the FORTRAN computing language. Indeed, it is the increased availability and rapid increase in computing power since the early 1990’s that has been a driver for the significant increase in the publication and citation of research into the use of Monte-Carlo for radiotherapy applications. Figure 1 shows the results of a Web of Science search (using the terms ‘Monte-Carlo’ AND ‘Radiotherapy’ OR ‘Radiation Therapy’) that reveals a total of 8419 publications which together have accumulated over 148,000 citations.

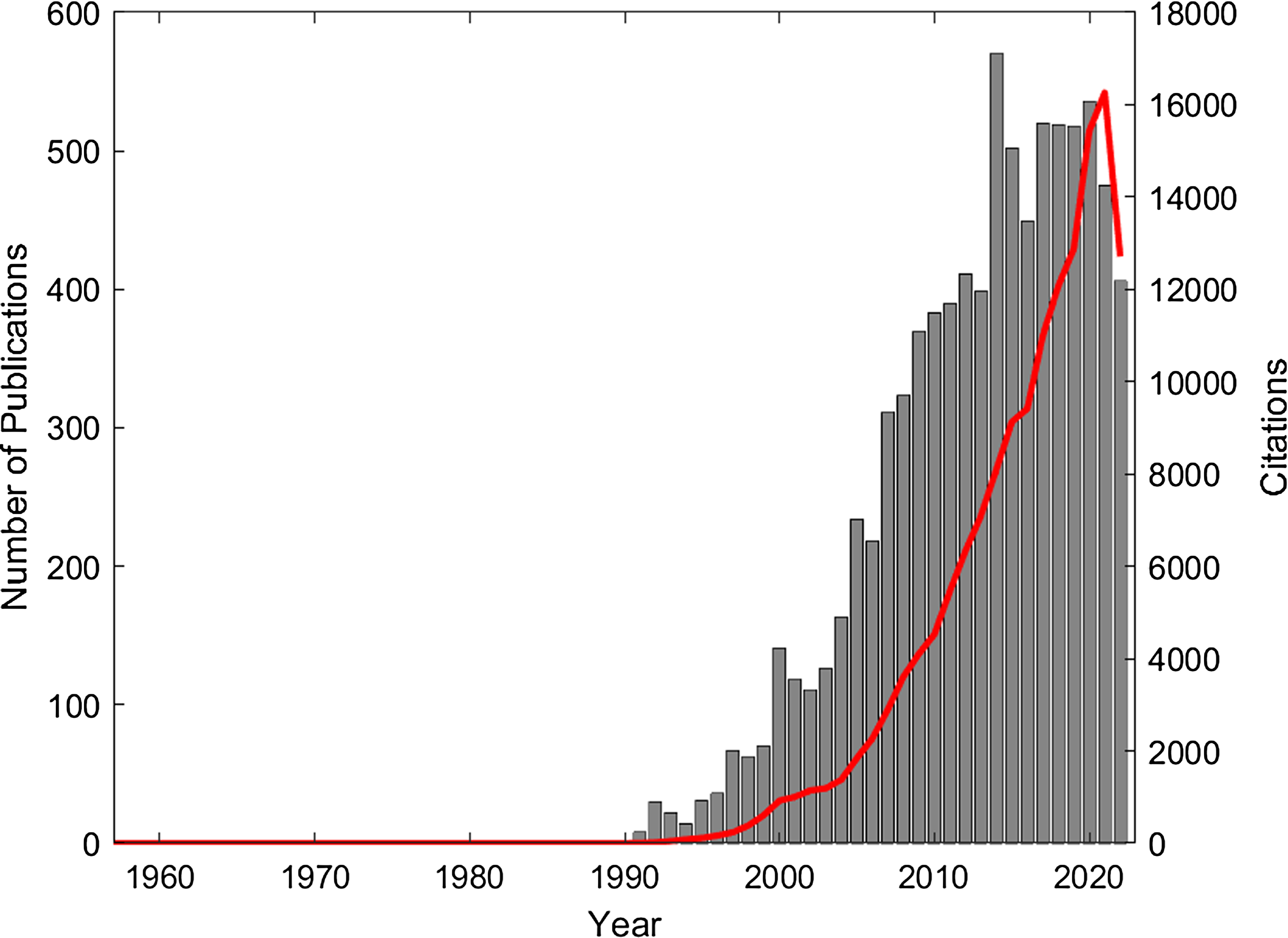
Figure 1. Publications (grey bar chart) and citations (red line) from 1957 to 2022 (Web of Science search terms: ‘monte carlo’ AND ‘Radiotherapy’ OR ‘Radiation Therapy’).

The main components of a Monte-Carlo ionising radiation transport simulation are the geometry, the physics models and the cross-section data representing the probabilities of the different physics occurring as a function of energy and material. Developing computer code that accurately encapsulates these three components, particularly for complex geometries is a serious undertaking. However, implementing a basic Monte-Carlo algorithm to model X-ray or gamma ray transport in simple geometries should be within the capabilities of most final-year physics, maths or engineering undergraduate students. The interested reader can find examples of simple implementations of the Monte-Carlo method in two interesting educational papers Reference Arqueros and Montesinos6,Reference Sharifzadeh, Afarideh, Khala and Gholipour7 . Fortunately, for those wishing to accurately model the detailed physics of the coupled X-ray and charged particle interactions in the complex geometries found in radiotherapy and medical imaging, a number of freely available codes are available that require relatively little programming experience. Additionally, Monte-Carlo algorithms are also now a common feature in most of the commercial radiotherapy treatment planning systems. Reference Chetty, Curran and Cygler8 This has made Monte-Carlo simulation accessible to those interested in the application of the technique to their own user-specific problem without having to go through the time-consuming process of developing code from scratch.

A constant caveat to the use of Monte-Carlo techniques for simulating radiotherapy treatments is the trade-off between statistical accuracy and the calculation time, known as the efficiency of the simulation. In the context of Monte-Carlo simulations, statistical accuracy is achieved by using a large number of random samples or particle ‘histories’ e.g. the number of electrons or X-rays, for radiation transport problems. As the number of histories is increased, the calculated quantities e.g. absorbed dose or fluence converge to those expected from real-world measurement. As well as the number of histories, other important factors that influence the statistical accuracy include the quality of the random number generator and the complexity of the physics and geometry models used in the simulation. Improvements in efficiency have been made through the use of variance reduction techniques and parallel processing using multiple Central Processing Unit (CPUs), and more recently, implementation on graphical processing units (GPUs). Reference Verhaegen and Seco9–Reference Jia, Gu, Graves, Folkerts and Jiang12 Variance reduction techniques are methods used to decrease the statistical variability (the variance) of calculated quantities such as absorbed dose or fluence without increasing the computational time, thus improving the efficiency of the use of computational resources.

In this first of two overview papers, we will begin by introducing the reader to the different Monte-Carlo codes that have been most widely used for modelling the different aspects of radiotherapy treatments. A companion paper will provide an overview of the main areas of application in radiotherapy, including modelling the production of beams of ionising radiation for radiotherapy and medical imaging, treatment verification, patient dosimetry and radiobiology.

Monte-Carlo codes

There are a number of Monte-Carlo codes that can be used to model the radiation transport problem. Short introductions to the codes that are freely available, still supported and most widely used in radiotherapy will now follow. It is acknowledged that there are other codes, such as VMC/VMC++ Reference Jia, Gu, Graves, Folkerts and Jiang12–Reference Sempau, Wilderman and Bielajew17 and DPM/gDPM, Reference Jia, Gu, Graves, Folkerts and Jiang12,Reference Sempau, Wilderman and Bielajew17 that have been developed and described in the literature over the years but are no longer freely available or supported as stand-alone codes. In some cases, they have been integrated into other more user-friendly or commercial treatment planning systems. The FLUKA code should also be acknowledged, as it is used extensively at CERN for modelling high energy particle physics and has also been used for simulating charged particle and heavy ion radiotherapy. Reference Böhlen, Cerutti and Chin18

EGSnrc/BEAMnrc/DOSXYZnrc

EGSnrc is one of the most widely used Monte-Carlo codes for radiotherapy and medical imaging applications. It is based on the Electron Gamma Shower (EGS) code developed at the Stanford Linear Accelerator (SLAC), Reference Nelson, Hirayama and Rogers19 and now maintained by the National Research Council of Canada, and distributed for free (https://github.com/nrc-cnrc/EGSnrc). The code runs on Linux, macOS and Windows operating systems and is able to model the transport of electrons, positrons and gammas with kinetic energies in the range 1 keV to 10 GeV. The code uses an implementation of the condensed history technique for charged particle propagation. Reference Kawrakow20 The code includes user codes with user-friendly graphical user interfaces that simplify the process of modelling the treatment heads of medical linear accelerators and performing patient dose calculations. BEAMnrc comprises component modules that facilitate the modelling of the geometry of components (e.g. target, primary collimator, flattening filter, jaws, MLC, etc.) found in the linear accelerator treatment head. Reference Rogers, Faddegon, Ding, Ma, We and Mackie21 DOSXYZnrc enables the calculation of dose deposited in voxelised rectilinear geometries including patient models derived from CT data. Reference Kawrakow and Walters22 The EGSnrc toolkit maintains flexibility through the inclusion of a wide range of C++ classes, known as egspp, that facilitate the modelling of more complex geometries,. Reference Kawrakow23

GEANT4

The GEANT4 toolkit was developed at CERN for modelling the passage of particles through matter Reference Agostinelli, Allison and Amako24–Reference Allison, Amako and Apostolakis26 (https://geant4.web.cern.ch/). Despite its original purpose being the simulation of high energy physics experiments and detectors, it has been extensively used for radiotherapy applications that include X-ray and particle beam therapy, micro and nano-dosimetry and radiation protection. Reference Arce, Bolst and Cutajar27 Electromagnetic physics is extended down to energies below 1 keV and up to the TeV range. Reference Chauvie, Guatelli and Ivanchenko28 The code is a C++ toolkit that makes use of contemporary object-oriented software engineering principles including the implementation of multi-threading on multi-core computer architectures. The power and flexibility that this design and implementation methodology gives GEANT4 come at the expense of the user being required to have significant prior knowledge and skills of developing applications using a modern C++ toolkit. This has limited its use in the radiotherapy community and has motivated the development of a number of more user friendly software tools that act as an interface or wrapper that makes GEANT4 more accessible to those without object-oriented programming expertise. These include GAMOS, Reference Arce, Rato, Canadas and Lagares29,Reference Arce, Lagares and Harkness30 GATE, Reference Jan, Benoit and Becheva31 PTSIM Reference Aso, Kimura, Kameoka, Murakami, Sasaki and Yamashita32,Reference Aso, Kimura, Yamashita and Sasaki33 and TOPAS. Reference Faddegon, Ramos-Méndez and Schuemann34,Reference Perl, Shin, Schumann, Faddegon and Paganetti35 A further advantage of the GEANT4 code is the GEANT4-DNA extension (http://geant4-dna.in2p3.fr/index.html) that enables modelling of the step-by-step discrete interactions of ionising particles in water at the cellular length scale. Reference Incerti, Baldacchino and Bernal36–Reference Incerti, Douglass, Penfold, Guatelli and Bezak38 Physical, chemical and biological effects of ionising radiation interactions in water can be modelled Reference Peukert, Incerti and Kempson39,Reference Sakata, Belov and Bordage40 using GEANT4-DNA.

GATE

The GEANT4 Application for Tomographic Emission (GATE) (http://www.opengatecollaboration.org/) is based on the GEANT4 toolkit and currently enables the simulation of Emission Tomography (PET and SPECT), computed tomography (CT), Bioluminescence and Fluorescence Imaging and Radiotherapy geometries. Reference Jan, Benoit and Becheva31,Reference Jan, Santin and Strul41–Reference Cuplov, Buvat, Pain and Jan44 GATE was originally developed for the nuclear medicine community with a primary aim of enabling the end user to model nuclear medicine systems without any requirement for prior knowledge of C++. Instead users use a more intuitive scripting language for creating geometries and setting simulation parameters that can then be run interactively or in batch mode. A feature of GATE is its capability for simulating dynamic or time-dependent aspects of an imaging experiment, for example, a decaying source, source and/or detector movement or breathing motion of a patient. Reference Santin, Strul and Lazaro45 In more recent times, GATE has been extended to include bioluminescence and optimal imaging Reference Cuplov, Buvat, Pain and Jan44,Reference Kang, Song, Han, Kim and Hong46 and radiotherapy, including particle therapy. Reference Jan, Benoit and Becheva31,Reference Sarrut, Bardiès and Boussion43,Reference Zarifi, Ahangari, Jia and Tajik-Mansoury47,Reference Zarifi, Ahangari, Jia, Tajik-Mansoury, Najafzadeh and Firouzjaei48

TOPAS

The TOPAS (Tool for PArticle Simulation) Monte-Carlo code was also developed to make it easier for the medical physicist to perform simulations of radiation transport using the GEANT4 code Reference Faddegon, Ramos-Méndez and Schuemann34,Reference Perl, Shin, Schumann, Faddegon and Paganetti35 (www.topasmc.org). Little or no knowledge of the GEANT4 code or the C++ programming language is required by the user. TOPAS simulations are controlled through a user-friendly TOPAS Parameter Control System that wraps the GEANT4 code while maintaining the full functionality of the underlying code including 4D time-dependent simulations. For more advanced users with C++ experience, there is the opportunity to develop their own extensions for integration into the TOPAS code. TOPAS was originally developed to facilitate the simulation of proton and carbon-ion therapy systems and has been used to develop models of passive and pencil beam scanning systems. Reference Liu, Zhang and Chen49–Reference Huang, Kang and Souris51 Despite its particle therapy roots, it is also able to model the more widely used photon and electron beams to the extent that an MV linac example is now included as part of the more recent releases. Examples of uses for modelling Brachytherapy sources are also provided. TOPAS has also been extended to include the Geant4-DNA radiobiology capabilities, Reference Schuemann, McNamara and Ramos-Méndez52–Reference McNamara, Geng and Turner55 through TOPAS-nBio (github.com/topas-nbio/TOPAS-nBio).

PENELOPE

PENELOPE is able to simulate electron and photon transport Reference Baró, Sempau, Fernández-Varea and Salvat56 utilising a mixed technique for modelling electron and positron collisions. The latest version, PENELOPE2018, is distributed by the OECD-NEA (https://www.oecd-nea.org/tools/abstract/detail/nea-1525/). The tools PENGEOM and penGUIn are available to simplify the definition of geometries and running simulations, respectively. PENELOPE has been successfully used to model medical linear accelerators through the extension PENLINAC Reference Rodríguez57 as well as the more specialised Tomotherapy Reference Sterpin, Salvat, Cravens, Ruchala, Olivera and Vynckier58,Reference Sterpin, Chen, Chen, Lu, Mackie and Vynckier59 and Leksell Gamma Knife systems. Reference Moskvin, DesRosiers, Papiez, Timmerman, Randall and DesRosiers60,Reference Moskvin, Timmerman and DesRosiers61

PRIMO

The PRIMO software (https://www.primoproject.net/primo/) enables the simulation of medical linear accelerators and patient dose calculations Reference Rodriguez, Sempau and Brualla62 using a user-friendly graphical interface. It is slightly different from other radiotherapy Monte-Carlo software in that it is available for free, but is not open source, instead being distributed as a compiled executable that runs in a 64-bit Windows environment. Parallel processing is supported on systems with multi-core processors. Reference Rodriguez and Brualla63 Beneath the intuitive graphical user interface, radiation transport is performed using the PENELOPE and DPM Monte-Carlo codes. Reference Sempau, Wilderman and Bielajew17,Reference Baró, Sempau, Fernández-Varea and Salvat56,Reference Rodriguez, Sempau, Bäumer, Timmermann and Brualla64

The ‘dose planning method’ (DPM) is a code for simulating the transport of electrons and photons in the context of radiotherapy. Reference Sempau, Wilderman and Bielajew17 The DPM code is designed to offer accurate 3D dose calculations in a fraction of the computational time of some of the other widely used codes. A mixed method for simulating electron and positron interactions is employed, with the choice of charged particle method (interaction-by-interaction or continual energy loss) chosen depending on the magnitude of the energy loss of the charged particle in the interaction. Photon interactions are modelled in an analogue manner.

Earlier versions (still available for download) of the PRIMO software supported both Elekta and Varian accelerator models, but recent versions only contain the Varian models that include a reverse-engineered TrueBeam model known as FakeBeam. Reference Rodriguez, Sempau, Fogliata, Cozzi, Sauerwein and Brualla65 Fakebeam models both flattening filter and flattening filter-free modes. Reference Belosi, Rodriguez and Fogliata66 PRIMO supports the import of DICOM RT Structure and Plan files enabling the simulation and evaluation of clinical IMRT and VMAT treatments. Reference Esposito, Silva, Oliveira, Lencart and Santos67,Reference Paganini, Reggiori and Stravato68 A further study also demonstrated the possibility of calculating patient dosimetry using Varian dynalog files. Reference Rodriguez and Brualla69 Comparisons of PRIMO with other Monte-Carlo codes have shown good agreement. Reference Aamri, Fielding and Aamry70,Reference Lloyd, Gagne, Bazalova-Carter and Zavgorodni71

MCNP

The Monte-Carlo N-Particle (MCNP) code (https://mcnp.lanl.gov/) is a general purpose radiation transport simulation code that is able to track 37 different particle types over a broad range of energies and up to 1 TeV/nucleon. Reference Kulesza, Adams and Armstrong72 The MCNP code is available to the worldwide user community, subject to USA national security restrictions and distributed through the Radiation Safety Information Computational Center, part of Oak Ridge National Laboratory. MCNP has been applied to a wide range of medical physics problems Reference Solberg, DeMarco and Chetty73 including the modelling of medical linear accelerators, Reference Mesbahi, Reilly and Thwaites74–Reference Kim, Siebers, Keall, Arnfield and Mohan78 and imaging systems such as radiotherapy electronic portal imaging devices (EPIDs), Reference Juste, Miro, Diez, Campayo and Verdu79–Reference Juste, Miró, Morera, Díez, Campayo and Verdú81 CT Reference Ding, Gu, Trofimov and Xu82 and PET/CT. Reference Waeleh, Saripan, Musarudin, Mashohor and Ahmad Saad83 MCNP has also been used to develop models for kV intraoperative radiotherapy, Reference Aghdam, Baghani, Mahdavi, Aghamiri and Akbari84,Reference Aghdam, Siavashpour, Aghamiri, Mahdavi and Nafisi85 Brachytherapy, Reference Furstoss, Reniers and Poon86–Reference Reniers, Verhaegen and Vynckier88 proton therapy Reference Jette and Chen89,Reference Verburg, Shih and Seco90 and gamma irradiator devices Reference Rodrigues, Grynberg and Ferreira91,Reference Moradi, Khandaker, Abdul Sani, Uguru, Sulieman and Bradley92 including the Leksell Gamma Knife Reference Trnka, Novotny and Kluson93,Reference Banaee, Asgari and Nedaie94

Conclusions

This paper is the first of two to give an overview of the use of Monte-Carlo simulation techniques and their application to radiotherapy. This first part has introduced the different codes that are available and currently supported with the aim of assisting the reader who wishes to develop their own use of Monte-Carlo for clinical or research applications. It is worth noting that many of the commercially available treatment planning systems, including Raystation (RaySearch Laboratories), Eclipse (Varian Medical Systems) and Monaco (Elekta) also now have Monte-Carlo algorithms as part of a suite of algorithms for electron, photon and more recently proton beams. Reference Paudel, Kim and Sarfehnia11,Reference Ali, Alsbou and Ahmad95–Reference Richmond, Angerud, Tamm and Allen97 Acceptable computational processing times are in some cases achieved through the implementation of these algorithms using GPU technology. The result as we move forward is that the radiotherapy practitioner will increasingly find themselves using Monte-Carlo techniques as part of treatment planning and treatment verification.

References

Metropolis, N, Ulam, S. The Monte Carlo method. J Am Stat Assoc 1949; 44 (247): 335–341.CrossRefGoogle ScholarPubMed
Duderstadt, JJ, Martin, WM. Transport Theory. New York: Wiley; 1979.Google Scholar
do Amaral Rodriguez, BD, Vilhena, MT. An overview of the boltzmann transport equation solution for neutrons, photons and electrons in cartesian geometry. 2009 International Nuclear Atlantic Conference - INAC 2009. Brazilian Association for Nuclear Energy. 2009.Google Scholar
Bruce, WR, Johns, HE. Monte Carlo calculations on the spectrum of scattered radiation produced in water by x-ray beams of interest in radiotherapy. Radiology 1957; 68 (1): 100–101.CrossRefGoogle Scholar
Berger, MJ. Monte Carlo calculation of the penetration and diffusion of fast charged particles. Methods Comput Physics 1963; 1: 135–215.Google Scholar
Arqueros, F, Montesinos, GD. A simple algorithm for the transport of gamma rays in a medium. Am J Phys 2003; 71 (1): 38.CrossRefGoogle Scholar
Sharifzadeh, M, Afarideh, H, Khala, H, Gholipour, R. A Matlab-Based Monte Carlo algorithm for transport of gamma-rays in matter. Monte Carlo Methods Appl 2015; 21 (1): 77–90.CrossRefGoogle Scholar
Chetty, IJ, Curran, B, Cygler, JE et al. Report of the AAPM Task Group No. 105: issues associated with clinical implementation of Monte Carlo-based photon and electron external beam treatment planning. Med Phys 2007; 34 (12): 4818–4853.CrossRefGoogle ScholarPubMed
Verhaegen, F, Seco, J. Monte Carlo Techniques in Radiation Therapy : Introduction, Source Modelling, and Patient Dose Calculations. Boca Raton: Taylor & Francis Group; 2021.CrossRefGoogle Scholar
Seco, J, Verhaegen, F. Monte Carlo Techniques in Radiation Therapy : Applications to Dosimetry, Imaging, and Preclinical Radiotherapy. Boca Raton: Taylor & Francis Group; 2021.CrossRefGoogle Scholar
Paudel, MR, Kim, A, Sarfehnia, A et al. Experimental evaluation of a GPU-based Monte Carlo dose calculation algorithm in the Monaco treatment planning system. J Appl Clin Med Phys 2016; 17 (6): 230–241.CrossRefGoogle ScholarPubMed
Jia, X, Gu, X, Graves, YJ, Folkerts, M, Jiang, SB. GPU-based fast Monte Carlo simulation for radiotherapy dose calculation. Phys Med Biol 2011; 56 (22): 7017–7031.CrossRefGoogle ScholarPubMed
Edimo, P, Clermont, C, Kwato, MG, Vynckier, S. Evaluation of a commercial VMC plus Monte Carlo based treatment planning system for electron beams using EGSnrc/BEAMnrc simulations and measurements. Phys Med 2009; 25 (3): 111–121.CrossRefGoogle Scholar
Fippel, M. Fast Monte Carlo dose calculation for photon beams based on the VMC electron algorithm. Med Phys 1999; 26 (8): 1466–1475.CrossRefGoogle ScholarPubMed
Gardner, J, Sievers, J, Kawrakow, I. Dose calculation validation of VMC++ for photon beams. Med Phys 2007; 34 (5): 1809–1818.CrossRefGoogle ScholarPubMed
Ferretti, A, Martignano, A, Simonato, F, Paiusco, M. Validation of a commercial TPS based on the VMC (++) Monte Carlo code for electron beams: commissioning and dosimetric comparison with EGSnrc in homogeneous and heterogeneous phantoms. Phys Med 2014; 30 (1): 25–35.CrossRefGoogle ScholarPubMed
Sempau, J, Wilderman, SJ, Bielajew, AF. DPM, a fast, accurate Monte Carlo code optimized for photon and electron radiotherapy treatment planning dose calculations. Phys Med Biol 2000; 45 (8): 2263–2291.CrossRefGoogle ScholarPubMed
Böhlen, TT, Cerutti, F, Chin, MPW et al. The FLUKA code: developments and challenges for high energy and medical applications. Nucl Data Sheets 2014; 120: 211–214.CrossRefGoogle Scholar
Nelson, WR, Hirayama, H, Rogers, DWO. The EGS4 code system, Report SLAC-265. Standford: Stanford Linear Accelerator Center, 1985.Google Scholar
Kawrakow, I. Accurate condensed history Monte Carlo simulation of electron transport. I. EGSnrc, the new EGS4 version. Med Phys 2000; 27 (3): 485–498.CrossRefGoogle ScholarPubMed
Rogers, DW, Faddegon, BA, Ding, GX, Ma, CM, We, J, Mackie, TR. BEAM: a Monte Carlo code to simulate radiotherapy treatment units. Med Phys 1995; 22 (5): 503–524.CrossRefGoogle Scholar
Kawrakow, I, Walters, BRB. Efficient photon beam dose calculations using DOSXYZnrc with BEAMnrc. Med Phys 2006; 33 (8): 3046–3056.CrossRefGoogle ScholarPubMed
Kawrakow, I. Egspp: The EGSnrc C++ Class Library. NRCC, 2019. https://nrc-cnrc.github.io/EGSnrc/doc/pirs898/. Accessed on 10th September 2022.Google Scholar
Agostinelli, S, Allison, J, Amako, K et al. Geant4—a simulation toolkit. Nucl Instrum Methods Phys Res A 2003; 506 (3): 250–303.CrossRefGoogle Scholar
Allison, J, Amako, K, Apostolakis, J et al. Geant4 developments and applications. IEE Trans Nucl Sci 2006; 53 (1): 270–278.CrossRefGoogle Scholar
Allison, J, Amako, K, Apostolakis, J et al. Recent developments in Geant4. Nucl Instrum Methods Phys Res A 2016; 835: 186–225.CrossRefGoogle Scholar
Arce, P, Bolst, D, Cutajar, D et al. Report on G4-Med, a Geant4 benchmarking system for medical physics applications developed by the Geant4 Medical Simulation Benchmarking Group. Med Phys 2020; 48 (1): 19–56. doi: 10.1002/mp.14226 CrossRefGoogle ScholarPubMed
Chauvie, S, Guatelli, S, Ivanchenko, V et al. Geant4 low energy electromagnetic physics. IEEE Symposium Conference Record Nuclear Science 2004; 3: 1881–1885.Google Scholar
Arce, P, Rato, P, Canadas, M, Lagares, JI. GAMOS: A Geant4-based easy and flexible framework for nuclear medicine applications. 2008 IEEE Nuclear Science Symposium Conference Record. 2008. 3162–3168.CrossRefGoogle Scholar
Arce, P, Lagares, JI, Harkness, L et al. GAMOS: An easy and flexible way to use GEANT4. 2011 IEEE Nuclear Science Symposium Conference Record. 2011. 2230–2237.CrossRefGoogle Scholar
Jan, S, Benoit, D, Becheva, E et al. GATE V6: a major enhancement of the GATE simulation platform enabling modelling of CT and radiotherapy. Phys Med Biol 2011; 56 (4): 881–901.CrossRefGoogle Scholar
Aso, T, Kimura, A, Kameoka, S, Murakami, K, Sasaki, T, Yamashita, T. GEANT4 based simulation framework for particle therapy system. 2007 IEEE Nuclear Science Symposium Conference Record, vol 4. 2007. 2564–2567.Google Scholar
Aso, T, Kimura, A, Yamashita, T, Sasaki, T. Optimization of patient geometry based on CT data in GEANT4 for medical application. 2007 IEEE Nuclear Science Symposium Conference Record, vol 4. 2007. 2576–2580.Google Scholar
Faddegon, B, Ramos-Méndez, J, Schuemann, J et al. The TOPAS tool for particle simulation, a Monte Carlo simulation tool for physics, biology and clinical research. Phys Med 2020; 72: 114–121.CrossRefGoogle ScholarPubMed
Perl, J, Shin, J, Schumann, J, Faddegon, B, Paganetti, H. TOPAS: an innovative proton Monte Carlo platform for research and clinical applications. Med Phys 2012; 39 (11): 6818–6837.CrossRefGoogle ScholarPubMed
Incerti, S, Baldacchino, G, Bernal, M et al. The Geant4-DNA project. Int J Modeling, Simulation, Sci Computing 2010; 01 (02): 157–178.CrossRefGoogle Scholar
Bernal, MA, Bordage, MC, Brown, JMC et al. Track structure modeling in liquid water: a review of the Geant4-DNA very low energy extension of the Geant4 Monte Carlo simulation toolkit. Phys Med 2015; 31 (8): 861–874.CrossRefGoogle Scholar
Incerti, S, Douglass, M, Penfold, S, Guatelli, S, Bezak, E. Review of Geant4-DNA applications for micro and nanoscale simulations. Phys Med 2016; 32 (10): 1187–1200.CrossRefGoogle ScholarPubMed
Peukert, D, Incerti, S, Kempson, I et al. Validation and investigation of reactive species yields of Geant4-DNA chemistry models. Med Phys 2019; 46 (2): 983–998.CrossRefGoogle ScholarPubMed
Sakata, D, Belov, O, Bordage, MC et al. Fully integrated Monte Carlo simulation for evaluating radiation induced DNA damage and subsequent repair using Geant4-DNA. Sci Rep 2020; 10 (1): 20788.CrossRefGoogle ScholarPubMed
Jan, S, Santin, G, Strul, D et al. GATE: a simulation toolkit for PET and SPECT. Phys Med Biol 2004; 49 (19): 4543–4561.CrossRefGoogle Scholar
Sarrut, D, Bała, M, Bardiès, M et al. Advanced Monte Carlo simulations of emission tomography imaging systems with GATE. Phys Med Biol 2021; 66 (10). doi: 10.1088/1361-6560/abf276 CrossRefGoogle ScholarPubMed
Sarrut, D, Bardiès, M, Boussion, N et al. A review of the use and potential of the GATE Monte Carlo simulation code for radiation therapy and dosimetry applications. Med Phys 2014; 41 (6): 064301.CrossRefGoogle ScholarPubMed
Cuplov, V, Buvat, I, Pain, F, Jan, S. Extension of the GATE Monte-Carlo simulation package to model bioluminescence and fluorescence imaging. J Biomed Opt 2014; 19 (2): 026004.CrossRefGoogle ScholarPubMed
Santin, G, Strul, D, Lazaro, D et al. GATE: a Geant4-based simulation platform for PET and SPECT integrating movement and time management. IEE Trans Nucl Sci 2003; 50 (5): 1516–1521.CrossRefGoogle Scholar
Kang, HG, Song, SH, Han, YB, Kim, KM, Hong, SJ. Lens implementation on the GATE Monte Carlo toolkit for optical imaging simulation. J Biomed Opt 2018; 23 (2): 1–13.Google ScholarPubMed
Zarifi, S, Ahangari, HT, Jia, SB, Tajik-Mansoury, MA. Validation of GATE Monte Carlo code for simulation of proton therapy using National Institute of Standards and Technology library data. J Radiother Pract 2019; 18 (1): 38–45.CrossRefGoogle Scholar
Zarifi, S, Ahangari, HT, Jia, SB, Tajik-Mansoury, MA, Najafzadeh, M, Firouzjaei, MP. Bragg peak characteristics of proton beams within therapeutic energy range and the comparison of stopping power using the GATE Monte Carlo simulation and the NIST data. J Radiother Pract 2020; 19 (2): 173–181.CrossRefGoogle Scholar
Liu, H, Zhang, L, Chen, Z et al. A preliminary Monte Carlo study for the treatment head of a carbon-ion radiotherapy facility using TOPAS. EPJ Web Conf 2017; 153: 04018.CrossRefGoogle Scholar
Lin, L, Kang, M, Solberg, TD, Ainsley, CG, McDonough, JE. Experimentally validated pencil beam scanning source model in TOPAS. Phys Med Biol 2014; 59 (22): 6859–6873.CrossRefGoogle ScholarPubMed
Huang, S, Kang, M, Souris, K et al. Validation and clinical implementation of an accurate Monte Carlo code for pencil beam scanning proton therapy. J Appl Clin Med Phys 2018; 19 (5): 558–572.CrossRefGoogle ScholarPubMed
Schuemann, J, McNamara, AL, Ramos-Méndez, J et al. TOPAS-nBio: an Extension to the TOPAS Simulation Toolkit for Cellular and Sub-cellular Radiobiology. Radiat Res 2019; 191 (2): 125–138.CrossRefGoogle Scholar
Ramos-Méndez, J, Perl, J, Schuemann, J, McNamara, A, Paganetti, H, Faddegon, B. Monte Carlo simulation of chemistry following radiolysis with TOPAS-nBio. Phys Med Biol 2018; 63 (10): 105014.CrossRefGoogle ScholarPubMed
McNamara, AL, Ramos-Méndez, J, Perl, J et al. Geometrical structures for radiation biology research as implemented in the TOPAS-nBio toolkit. Phys Med Biol 2018; 63 (17): 175018.CrossRefGoogle ScholarPubMed
McNamara, A, Geng, C, Turner, R et al. Validation of the radiobiology toolkit TOPAS-nBio in simple DNA geometries. Phys Med 2017; 33: 207–215.CrossRefGoogle ScholarPubMed
Baró, J, Sempau, J, Fernández-Varea, JM, Salvat, F. PENELOPE: an algorithm for Monte Carlo simulation of the penetration and energy loss of electrons and positrons in matter. Nucl Instrum Methods Phys Res B 1995; 100 (1): 31–46.CrossRefGoogle Scholar
Rodríguez, ML. PENLINAC: extending the capabilities of the Monte Carlo code PENELOPE for the simulation of therapeutic beams. Phys Med Biol 2008; 53 (17): 4573–4593.CrossRefGoogle ScholarPubMed
Sterpin, E, Salvat, F, Cravens, R, Ruchala, K, Olivera, GH, Vynckier, S. Monte Carlo simulation of helical tomotherapy with PENELOPE. Phys Med Biol 2008; 53 (8): 2161–2180.CrossRefGoogle ScholarPubMed
Sterpin, E, Chen, Y, Chen, Q, Lu, W, Mackie, TR, Vynckier, S. Monte Carlo-based simulation of dynamic jaws tomotherapy. Med Phys 2011; 38 (9): 5230–5238.CrossRefGoogle ScholarPubMed
Moskvin, V, DesRosiers, C, Papiez, L, Timmerman, R, Randall, M, DesRosiers, P. Monte Carlo simulation of the Leksell Gamma Knife: I. Source modelling and calculations in homogeneous media. Phys Med Biol 2002; 47 (12): 1995–2011.CrossRefGoogle ScholarPubMed
Moskvin, V, Timmerman, R, DesRosiers, C et al. Monte carlo simulation of the Leksell Gamma Knife: II. Effects of heterogeneous versus homogeneous media for stereotactic radiosurgery. Phys Med Biol 2004; 49 (21): 4879–4895.CrossRefGoogle ScholarPubMed
Rodriguez, M, Sempau, J, Brualla, L. PRIMO: a graphical environment for the Monte Carlo simulation of Varian and Elekta linacs. Strahlenther Onkol 2013; 189 (10): 881–886.CrossRefGoogle Scholar
Rodriguez, M, Brualla, L. Many-integrated core (MIC) technology for accelerating Monte Carlo simulation of radiation transport: a study based on the code DPM. Comput Phys Commun 2018; 225: 28–35.CrossRefGoogle Scholar
Rodriguez, M, Sempau, J, Bäumer, C, Timmermann, B, Brualla, L. DPM as a radiation transport engine for PRIMO. Radiat Oncol 2018; 13 (1): 256.CrossRefGoogle ScholarPubMed
Rodriguez, M, Sempau, J, Fogliata, A, Cozzi, L, Sauerwein, W, Brualla, L. A geometrical model for the Monte Carlo simulation of the TrueBeam linac. Phys Med Biol 2015; 60 (11): N219–N229.CrossRefGoogle ScholarPubMed
Belosi, MF, Rodriguez, M, Fogliata, A et al. Monte Carlo simulation of TrueBeam flattening-filter-free beams using varian phase-space files: comparison with experimental data. Med Phys 2014; 41 (5): 051707.CrossRefGoogle ScholarPubMed
Esposito, A, Silva, S, Oliveira, J, Lencart, J, Santos, J. Primo software as a tool for Monte Carlo simulations of intensity modulated radiotherapy: a feasibility study. Radiat Oncol 2018; 13 (1): 91.CrossRefGoogle ScholarPubMed
Paganini, L, Reggiori, G, Stravato, A et al. MLC parameters from static fields to VMAT plans: an evaluation in a RT-dedicated MC environment (PRIMO). Radiat Oncol 2019; 14 (1): 216.CrossRefGoogle Scholar
Rodriguez, M, Brualla, L. Treatment verification using Varian’s dynalog files in the Monte Carlo system PRIMO. Radiat Oncol 2019; 14 (1): 67.CrossRefGoogle ScholarPubMed
Aamri, H, Fielding, A, Aamry, A et al. Comparison between PRIMO and EGSnrc Monte Carlo models of the Varian True Beam linear accelerator. Radiat Phys Chem 2020; 178: 109013.CrossRefGoogle Scholar
Lloyd, SAM, Gagne, IM, Bazalova-Carter, M, Zavgorodni, S. Validation of Varian TrueBeam electron phase-spaces for Monte Carlo simulation of MLC-shaped fields. Med Phys 2016; 43 (6): 2894–2903.CrossRefGoogle ScholarPubMed
Kulesza, J, Adams, T, Armstrong, J et al. MCNP® Code Version 6.3.0 Theory & User Manual. Boca Raton: Office of Scientific and Technical Information (OSTI), 2022. doi: 10.2172/1889957 Google Scholar
Solberg, TD, DeMarco, JJ, Chetty, IJ et al. A review of radiation dosimetry applications using the MCNP Monte Carlo code. Radiochim Acta 2001; 89 (4–5): 337–355.CrossRefGoogle Scholar
Mesbahi, A, Reilly, AJ, Thwaites, DI. Development and commissioning of a Monte Carlo photon beam model for Varian Clinac 2100EX linear accelerator. Appl Radiat Isot 2006; 64 (6): 656–662.CrossRefGoogle ScholarPubMed
Ezzati, AO, Studenski, MT, Jamshidi, N. A simple source model for 6 MV flattening filter free photon beams Monte Carlo dose calculations. Phys Part Nucl Lett 2021; 18 (7): 791–798.CrossRefGoogle Scholar
Padilla-Cabal, F, Pérez-Liva, M, Lara, E, Alfonso, R, Lopez-Pino, N. Monte Carlo calculations of an Elekta Precise SL-25 photon beam model. J Radiother Pract 2015; 14 (3): 1–12.CrossRefGoogle Scholar
Bahreyni Toossi, MT, Ghorbani, M, Akbari, F, Sabet, LS, Mehrpouyan, M. Monte Carlo simulation of electron modes of a Siemens Primus linac (8, 12 and 14 MeV). J Radiother Pract 2013; 12 (4): 352–359.CrossRefGoogle Scholar
Kim, JO, Siebers, JV, Keall, PJ, Arnfield, MR, Mohan, R. A Monte Carlo study of radiation transport through multileaf collimators. Med Phys 2001; 28 (12): 2497–2506.CrossRefGoogle ScholarPubMed
Juste, B, Miro, R, Diez, S, Campayo, JM, Verdu, G. Monte Carlo simulation of the iView GT portal imager dosimetry. 7th International Topical Meeting on Industrial Radiation and Radioisotope Measurement Application, vol 68. 2010. 922–925.CrossRefGoogle Scholar
Juste, B, Miro, R, Diez, S, Campayo, JM, Verdu, G. Dosimetric capabilities of the Iview GT portal imager using MCNP5 monte carlo simulations. 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, vol 2009. Embc: 2009 Annual International Conference of the Ieee Engineering in Medicine and Biology Society, vol 1–20. 2009. 3743–3746.Google Scholar
Juste, B, Miró, R, Morera, D, Díez, S, Campayo, J, Verdú, G. MCNP5 Monte Carlo simulation of amorphous silicon EPID dosimetry from MLC radiation therapy treatment beams. 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society Conference Proceedings. 2012. 5786–5789.CrossRefGoogle Scholar
Ding, AP, Gu, JW, Trofimov, AV, Xu, XG. Monte Carlo calculation of imaging doses from diagnostic multidetector CT and kilovoltage cone-beam CT as part of prostate cancer treatment plans. Med Phys 2010; 37 (12): 6199–6204.CrossRefGoogle ScholarPubMed
Waeleh, N, Saripan, MI, Musarudin, M, Mashohor, S, Ahmad Saad, FF. Modeling and experimental verification of Biograph TruePoint PET/CT using MCNP5. 2020 IEEE-EMBS Conference on Biomedical Engineering and Sciences (IECBES). ieeexplore.ieee.org. 2021. 319–323.CrossRefGoogle Scholar
Aghdam, MRH, Baghani, HR, Mahdavi, SR, Aghamiri, SMR, Akbari, ME. Monte Carlo study on effective source to surface distance for electron beams from a mobile dedicated IORT accelerator. J Radiother Pract 2017; 16 (1): 29–37.CrossRefGoogle Scholar
Aghdam, SRH, Siavashpour, Z, Aghamiri, SMR, Mahdavi, SR, Nafisi, N. Evaluating the radiation contamination dose around a high dose per pulse intraoperative radiotherapy accelerator: a Monte Carlo study. J Radiother Pract 2020; 19 (3): 265–276.CrossRefGoogle Scholar
Furstoss, C, Reniers, B, Poon, E et al. Monte Carlo iodine brachytherapy dosimetry: study for a clinical application. J Phys Conf Ser 2008; 102.CrossRefGoogle Scholar
Solc, J. Monte Carlo calculation of dose to water of a (106)Ru COB-type ophthalmic plaque. J Phys Conf Ser 2008; 102.CrossRefGoogle Scholar
Reniers, B, Verhaegen, F, Vynckier, S. The radial dose function of low-energy brachytherapy seeds in different solid phantoms: comparison between calculations with the EGSnrc and MCNP4C Monte Carlo codes and measurements. Phys Med Biol 2004; 49 (8): 1569–1582.CrossRefGoogle ScholarPubMed
Jette, D, Chen, W. Creating a spread-out Bragg peak in proton beams. Phys Med Biol 2011; 56 (11): N131–N138.CrossRefGoogle ScholarPubMed
Verburg, JM, Shih, HA, Seco, J. Simulation of prompt gamma-ray emission during proton radiotherapy. Phys Med Biol 2012; 57 (17): 5459–5472.CrossRefGoogle ScholarPubMed
Rodrigues, RR, Grynberg, SE, Ferreira, AV et al. Retrieval of GammaCell 220 irradiator isodose curves with MCNP simulations and experimental measurements. Braz J Phys 2010; 40 (1): 120–124.CrossRefGoogle Scholar
Moradi, F, Khandaker, MU, Abdul Sani, SF, Uguru, EH, Sulieman, A, Bradley, DA. Feasibility study of a minibeam collimator design for a 60Co gamma irradiator. Radiat Phys Chem 2021; 178: 109026.CrossRefGoogle Scholar
Trnka, J, Novotny, J Jr, Kluson, J. MCNP-based computational model for the Leksell gamma knife. Med Phys 2007; 34 (1): 63–75.CrossRefGoogle ScholarPubMed
Banaee, N, Asgari, S, Nedaie, HA. Comparison of penumbra regions produced by ancient Gamma knife model C and Gamma ART 6000 using Monte Carlo MCNP6 simulation. Appl Radiat Isot 2018; 137: 154–160.CrossRefGoogle Scholar
Ali, I, Alsbou, N, Ahmad, S. Quantitative evaluation of dosimetric uncertainties in electron therapy by measurement and calculation using the electron Monte Carlo dose algorithm in the Eclipse treatment planning system. J Appl Clin Med Phys 2022; 23 (1): e13478.CrossRefGoogle ScholarPubMed
Richmond, N, Allen, V, Wyatt, J, Codling, R. Evaluation of the RayStation electron Monte Carlo dose calculation algorithm. Med Dosim 2020; 45 (2): 159–167.CrossRefGoogle ScholarPubMed
Richmond, N, Angerud, A, Tamm, F, Allen, V. Comparison of the RayStation photon Monte Carlo dose calculation algorithm against measured data under homogeneous and heterogeneous irradiation geometries. Phys Med 2021; 82: 87–99.CrossRefGoogle ScholarPubMed
Figure 0

Figure 1. Publications (grey bar chart) and citations (red line) from 1957 to 2022 (Web of Science search terms: ‘monte carlo’ AND ‘Radiotherapy’ OR ‘Radiation Therapy’).