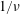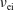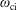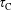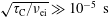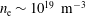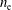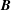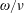Letter
Understanding the turbulent mechanisms setting the density decay length in the tokamak scrape-off layer
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2020, 175860101
-
- Article
-
- You have access
- HTML
- Export citation
- NASA ADS Abstract Service
Letter
Effect of plasma elongation on current dynamics during tokamak disruptions
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2020, 474860101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Research Article
Enhancement of laser-driven ion acceleration in non-periodic nanostructured targets
-
- Published online by Cambridge University Press:
- 17 January 2020, 905860101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Development of a non-parametric Gaussian process model in the three-dimensional equilibrium reconstruction code V3FIT
- Part of:
-
- Published online by Cambridge University Press:
- 13 January 2020, 905860102
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Adjoint approach to calculating shape gradients for three-dimensional magnetic confinement equilibria. Part 2. Applications
- Part of:
-
- Published online by Cambridge University Press:
- 13 January 2020, 905860103
Electron skin depth in low density plasmas
-
- Published online by Cambridge University Press:
- 13 January 2020, 905860104
Bootstrap current and parallel ion velocity in imperfectly optimized stellarators
- Part of:
-
- Published online by Cambridge University Press:
- 13 January 2020, 905860105
Near-axis expansion of stellarator equilibrium at arbitrary order in the distance to the axis
- Part of:
-
- Published online by Cambridge University Press:
- 28 January 2020, 905860106
General three-dimensional equilibria for gravitating ideal magnetohydrodynamics of field-aligned steady incompressible flows with an application to solar prominences
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2020, 905860107
On the deviation from Maxwellian of the ion velocity distribution functions in the turbulent magnetosheath
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2020, 905860108
-
- Article
-
- You have access
- HTML
- Export citation
- NASA ADS Abstract Service
Electromagnetic full-
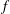 $f$ gyrokinetics in the tokamak edge with discontinuous Galerkin methods
$f$ gyrokinetics in the tokamak edge with discontinuous Galerkin methods
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2020, 905860109
-
- Article
-
- You have access
- HTML
- Export citation
- NASA ADS Abstract Service
The nature of mean-field generation in three classes of optimal dynamos
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2020, 905860110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Effect of the pressure of the dust grains in strongly coupled dusty plasma on the head-on collision between two nonlinear waves
-
- Published online by Cambridge University Press:
- 28 February 2020, 905860111
Tutorial
Differential forms for plasma physics
- Part of:
-
- Published online by Cambridge University Press:
- 13 January 2020, 925860101
-
- Article
-
- You have access
- HTML
- Export citation
- NASA ADS Abstract Service