For the simple model of cold electrons streaming against cold ions the complete set of nonlinear stationary waves is expressed in terms of elliptic functions. The conditions for their dynamical connection to a uniform neutral plasma state are taken into account, and the conditions for the neglect of the magnetic field are analysed. The range of existence of stationary waves is found to be confined to the stable regime of the two-stream instability, but covers only part of it. All nonlinear BGK waves that are found within the limits of the model can be shown to bifurcate from the two-stream instability, some of them also exhibiting secondary and further bifurcations. As an exceptional case, all bifurcations can be treated exactly. Close to the linear regime, all nonlinear modes turn out to be unstable. The corresponding instability is caused by a wave decay that transports energy from low to high wavenumbers of the Fourier modes constituting the wave. From the two-stream solutions four- stream solutions with exactly vanishing magnetic field are derived.

Magneto-acoustic instability driven by cosmic rays and the waves that they excite was first studied by McKenzie and Webb and by Zank. In the present paper this instability is reconsidered. In general, the cosmic-ray plasma system is unstable. However, depending on how the time scale is chosen, the results and interpretation may be different from those of McKenzie and Webb and of Zank, particularly in the long- and short-wavelength limits. To illustrate this instability in an astrophysical context, we take our Galaxy and supernova remnants as examples. In those examples, length scales shorter than 2.5 kpc and 1.5 pc respectively are susceptible to this instability, and the growth times are of the order of 4 × 108 and 1.5 × 104 yr respectively.

We have shown earlier that compressional magnetic fluctuations modify the properties of MHD waves. The modifications can be large even when the fluctuation level is much smaller than the ambient magnetic field. There are two kinds of effects: resonant and non-resonant. The former is a result of the so- called parametric cyclotron resonance, and enables energy transfer from the wave to particle Larmor motion. This transfer causes the damping of waves even when their frequency is so small that ordinary cyclotron damping is negligible. The non-resonant effect does not cause energy exchange, but it does modify wave dispersion and causes mode coupling between the shear Alfvén mode and magnetosonic modes.

A generalized non-local nonlinear Schrödinger equation describing the phenomenon of nonlinear Landau damping in a relativistic two-component plasma is deduced using the kinetic-theory approach of Vlasov. Parameters appearing in the equation are evaluated explicitly for the case of a Maxwellian distribution function.

The nonlinear dynamics of wave envelopes modulated in 2 + 1 dimensions is considered for two systems in plasma physics: (i) Langmuir pulses and (ii) intense (but weakly relativistic) electromagnetic (EM) pulses. Using singular perturbation techniques applied to an envelope approximation, both problems are reduced to the two-dimensional nonlinear Schrödinger (2DNLS) system, which describes the dynamics of two coupled slowly varying potentials. The general 2DNLS system exhibits a rich variety of phenomena, including enhanced (compared with ‘longitudinal’ propagation) modulational stability and (1D) soliton formation; decay of 1D solitons over long time scales; self- focusing regimes (determined by a virial-type condition); as well as integrability and 2D solitons. Applying our recent results on the 2DNLS system, we determine which of these phenomena can actually occur here and compute the parameter regimes. (i) The 2DNLS system for the Zakharov equations is modulationally unstable for all parameter values. It also has an integrable sector and a self-focusing regime. (ii) The 2DNLS system describes coupled ‘longitudinal’ and ‘transverse’ modulations of linearly or circularly polarized EM pulses propagating through a warm unmagnetized two-component neutral plasma with arbitrary masses (i.e. electron—positron or electron—ion). The pulse can accelerate particles to weakly (but not fully) relativistic velocities; relativistic, ponderomotive and harmonic effects all contribute to the nonlinear terms. The resulting 2DNLS system does not admit a self-focusing regime. Parameter values leading to an integrable case (the so-called ‘Davey—Stewartson I’ equations, which admit 2D soliton solutions) are computed; however, the required values would not be attainable in a laboratory or astrophysical setting. None the less, the existence of new nonlinear modulational instabilities associated with the second spatial degree of freedom already represents an important potential limitation on any (1 + 1)-dimensional approach to nonlinear evolution and modulational instability of plasma EM waves.

A mapping method is developed to investigate the problem of determination and control of heat-deposition patterns on the plates of a tokamak divertor. The deposition pattern is largely determined by the magnetic field lines, which are mathematically equivalent to the trajectories of a single-degree-of-freedom time-dependent Hamiltonian system. Maps are natural tools to study the generic features of such systems. The general theory of maps is presented, and methods for incorporating various features of the magnetic field and particle motion in divertor tokamaks are given. Features of the magnetic field include the profile of the rotational transform, single- versus double-null divertor, reverse map, the effects of naturally occurring low M and N, and externally imposed high-M, high-N perturbations. Particle motion includes radial diffusion, pitch angle and energy scattering, and the electric sheath at the plate. The method is illustrated by calculating the stochastic broadening in a single- null divertor tokamak. Maps provide an efficient, economic and elegant method to study the problem of motion of plasma particles in the stochastic scrape-off layer.

It is shown that rotation of a periodic column of magnetohydrodynamic fluid can be stabilized against current-driven instabilities by rotation. The rotation is considered as resulting from a slight departure from overall charge neutrality, and is braked by wall friction (loss of angular momentum to the cylinder wall). Both effects are modelled phenomenologically in the equation of motion, and the emphasis is on their bulk dynamic effects rather their microscopic kinetic theory origins. Much as rotation is known to stabilize a Navier—Stokes fluid against transverse displacements, it is shown that sufficient rotation will suppress the helical vortices and helical deformations of the current channel that are known to result when the axial current in the column exceeds its stability threshold.

A numerical technique, alternative to Grad's well-known ADM method has been proposed to deal with the slow adiabatic evolution of a toroidal plasma with flow. The equilibrium problem with prescribed adiabatic constraints may be solved by simultaneous calculations of flux surface geometry and original profile functions. Implications for the problem of bifurcation due to nonlinearity of the governing equations are discussed. In the case of field-aligned sub-Alfvénic flow the system is in the second elliptic regime if β <A2/(1 – A2) at the magnetic axis, where A is the Mach Alfvén number of the flow. Super-Alfvénic flows do not satisfy the local firehose stability criterion.

The paper explores the interrelationship between the generalized Grad-Shafranov equation, or trans-field force balance equation, for steady MHD flows with an ingnorable co-ordinate, and work by Imai on field-aligned MHD flows. The development of Imai, assumes at the outset that the fluid velocity V is parallel to the magnetic field B, and exploits an analogy with steady compressible irrotational flow in ordinary fluid dynamics. In Imai's analysis the magnetic induction B is written in the form B = σb, where 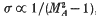, and MA is the appropriate Alfvén Mach number. Gauss' law Δ. B = Δ. (σb) = 0 then plays a role analogous to the mass continuity equation in ordinary fluid dynamics, where σ corresponds to the density of the pseudo-fluid. Imai's analysis leads to a transonic equation for the field potential φ defined by b = Δφ. For a restricted class of flows the trans-field force balance equation formulation also leads to the transonic potential flow equation, but the assumption of an ignorable co-ordinate allows for the possibility of non-field-aligned flows with non-zero electric field potential ΦE The characteristics of the generalized Grad—Shafranov equation are related to the Mach cone and the group velocity surface for linear magnetosonic waves. The corresponding forms of the characteristics for the potential transonic flow equation in the (x, y) plane and in the (bx, by) hodograph plane are discussed. Sample solutions of the potential transonic flow equation for radial, helical and spiral flows are obtained by means of the hodograph transformation, and are used to illustrate the differences between hyperbolic and elliptic flows. The potential transonic flow equation is obtained for the case of an ignorable co-ordinate z of a rectangular Cartesian co-ordinate system (x, y, z), and also for the case of flows with an ignorable co-ordinate of a spherical polar co-ordinate system (r, θ, ω). Astrophysical applications are briefly discussed.