The question of magnetic field structure in the vicinity of the separatrix in divertor tokamaks is studied. The authors have investigated this problem earlier in a series of papers, using various mathematical techniques. In the present paper, the two-wire model (TWM) [Reiman, A. 1996 Phys. Plasmas3, 906] is considered. It is noted that, in the TWM, it is useful to consider an extra equation expressing magnetic flux conservation. This equation does not add any more information to the TWM, since the equation is derived from the TWM. This equation is useful for controlling the step size in the numerical integration of the TWM equations. The TWM with the extra equation is called the flux-preserving TWM. Nevertheless, the technique is apparently still plagued by numerical inaccuracies when the perturbation level is low, resulting in an incorrect scaling of the stochastic layer width. The stochastic broadening of the separatrix in the flux-preserving TWM is compared with that in the low mn (poloidal mode number m and toroidal mode number n) map (LMN) [Ali, H., Punjabi, A., Boozer, A. and Evans, T. 2004 Phys. Plasmas11, 1908]. The flux-preserving TWM and LMN both give Boozer–Rechester 0.5 power scaling of the stochastic layer width with the amplitude of magnetic perturbation when the perturbation is sufficiently large [Boozer, A. and Rechester, A. 1978, Phys. Fluids21, 682]. The flux-preserving TWM gives a larger stochastic layer width when the perturbation is low, while the LMN gives correct scaling in the low perturbation region. Area-preserving maps such as the LMN respect the Hamiltonian structure of field line trajectories, and have the added advantage of computational efficiency. Also, for a 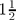 degree of freedom Hamiltonian system such as field lines, maps do not give Arnold diffusion.
degree of freedom Hamiltonian system such as field lines, maps do not give Arnold diffusion.


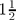 degree of freedom Hamiltonian system such as field lines, maps do not give Arnold diffusion.
degree of freedom Hamiltonian system such as field lines, maps do not give Arnold diffusion.